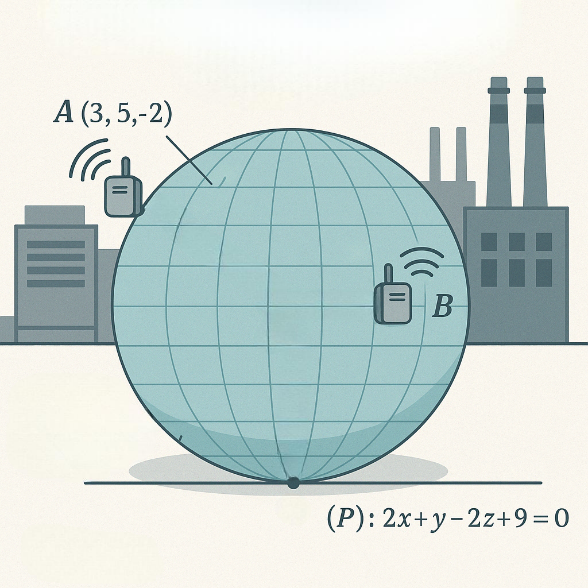
Một công ty xây dựng một hệ thống giám sát môi trường tại khu công nghiệp. Hai cảm biến không dây được đặt tại hai vị trí \(A,\,B\)trong không gian 3 chiều để thu thập dữ liệu không khí. Để đảm bảo tín hiệu truyền giữa hai cảm biến ổn định, công ty thiết kế một bóng bảo vệ tín hiệu hình cầu di động nhưng luôn đi qua cả hai cảm biến \(A\) và \(B\). Bóng này cần tiếp xúc với mặt đất để đảm bảo tính ổn định. Giả sử trong không gian với hệ toạ độ \(Oxyz\), toạ độ các điểm là \(A\left( {3;5; - 2} \right)\), \(B\left( { - 1;3;2} \right)\) và mặt đất được mô tả bằng mặt phẳng \(\left( P \right):2x + y - 2z + 9 = 0.\) Trong quá trình mô phỏng, điểm tiếp xúc giữa bóng bảo vệ và mặt đất (gọi là \(C\)) thay đổi. Kỹ sư cần xác định khoảng cách từ gốc tọa độ \(O\left( {0;0;0} \right)\) đến điểm tiếp xúc \(C\) để đánh giá mức độ ảnh hưởng từ vị trí đặt thiết bị. Gọi \({m_1}\) là giá trị lớn nhất và \({m_2}\) là giá trị nhỏ nhất của độ dài \(OC.\) Tính giá trị \({m_1}^2 + {m_2}^2.\)
Câu hỏi trong đề: Đề kiểm tra Toán 12 Cánh diều Chương 5 có đáp án !!
Quảng cáo
Trả lời:
Đáp án:
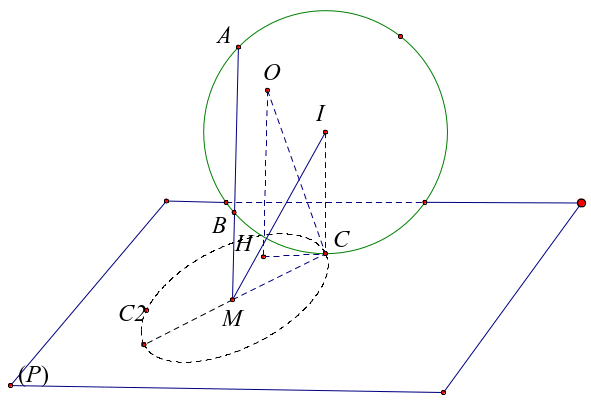
\(\left\{ \begin{array}{l}\overrightarrow {AB} = \left( { - 4; - 2;4} \right) = - 2\left( {2;1; - 2} \right)\\\overrightarrow {{n_P}} = \left( {2;1; - 2} \right)\end{array} \right.\)\( \Rightarrow \overrightarrow {AB} ,\;\overrightarrow {{n_P}} \) cùng phương nên \(\overrightarrow {AB} \bot \left( P \right)\), \(AB = 6\).
\(d\left( {A,\;\left( P \right)} \right) = \frac{{\left| {2.3 + 5 - 2.\left( { - 2} \right) + 9} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 2} \right)}^2}} }} = 8\) và \(d\left( {B,\;\left( P \right)} \right) = \frac{{\left| {2.\left( { - 1} \right) + 3 - 2.2 + 9} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 2} \right)}^2}} }} = 2\).
\(AB \cap \left( P \right) = M \Rightarrow M\) cố định.
Do \(\left( P \right)\) tiếp xúc với mặt cầu \(\left( S \right)\) tại \(C\) nên \(MC \bot IC\) tại \(C\).
\( \Rightarrow MA.MB = M{C^2}\), ta có: \(\left\{ \begin{array}{l}MA = d\left( {A;\;\left( P \right)} \right) = 8\\MB = d\left( {B;\left( P \right)} \right) = 2\end{array} \right. \Leftrightarrow M{C^2} = 16 \Leftrightarrow MC = 4\).
\( \Rightarrow C\) thuộc đường tròn tâm \(M\) bán kính \(r = MC = 4\).
Ta có: \(AB:\left\{ \begin{array}{l}x = 3 + 2t\\y = 5 + t\\z = - 2 - 2t\end{array} \right.\), \(M = AB \cap \left( P \right) \Rightarrow M\left( { - \frac{7}{3};\frac{7}{3};\frac{{10}}{3}} \right)\).
Gọi \(H\) là hình chiếu của \(O\) lên mặt phẳng \(\left( P \right)\) \( \Rightarrow d\left( {O\left( P \right)} \right) = 3\), \(OH:\left\{ \begin{array}{l}x = 2t\\y = t\\z = - 2t\end{array} \right.\).
\(H = OH \cap \left( P \right)\)\( \Leftrightarrow H\left( { - 2;\; - 1;\;2} \right)\), \(HM = \sqrt {13} < 4\) nên \(H\) nằm trong đường tròn tâm \(M\) bán kính \(r = MC = 4\). Suy ra \(OC = \sqrt {O{H^2} + H{C^2}} = \sqrt {9 + H{C^2}} \).
\( \Rightarrow OC\) đạt min hoặc max \( \Leftrightarrow HC\) đạt min hoặc max
\(\left\{ \begin{array}{l}H{C_{\min }} = \left| {HM - r} \right| = 4 - \sqrt {13} \\H{C_{\max }} = HM + r = 4 + \sqrt {13} \end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}O{C_{\min }} = \sqrt {9 + \left( {4 - {{\sqrt {13} }^2}} \right)} = {m_2}\\O{C_{\max }} = \sqrt {9 + {{\left( {4 + \sqrt {13} } \right)}^2}} = {m_1}\end{array} \right.\).
Vậy \({m_1}^2 + {m_2}^2 = 76\).
Đáp án: 76.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(\left| {\overrightarrow {{v_1}} } \right| = \sqrt {{3^2} + {4^2} + {0^2}} = 5\), \(\left| {\overrightarrow {{v_2}} } \right| = \sqrt {{5^2} + {{12}^2} + {0^2}} = 13\), \(\left| {\overrightarrow u } \right| = \sqrt {{{\left( { - 3} \right)}^2} + {0^2} + {4^2}} = 5\).
Vận tốc thực tế của máy bay Su-30 là \(\overrightarrow {{V_1}} = \frac{{900}}{{\left| {\overrightarrow {{v_1}} } \right|}}\overrightarrow {{v_1}} + \frac{{80}}{{\left| {\overrightarrow u } \right|}}\overrightarrow u \) \( = \left( {492;720;64} \right)\).
Phương trình chuyển động của máy bay Su-30 là: \(\left\{ \begin{array}{l}x = 492t\\y = 35 + 720t\\z = 10 + 64t\end{array} \right.\).
Vận tốc thực tế của máy bay MiG-31 là \(\overrightarrow {{V_2}} = \frac{{910}}{{\left| {\overrightarrow {{v_2}} } \right|}}\overrightarrow {{v_2}} + \frac{{80}}{{\left| {\overrightarrow u } \right|}}\overrightarrow u \) \( = \left( {302;840;64} \right)\).
Phương trình chuyển động của máy bay MiG-31 là: \(\left\{ \begin{array}{l}x = 31 + 302t\\y = 10 + 840t\\z = 11 + 64t\end{array} \right.\).
Khu vực không phận bị hạn chế là \(\left\{ \begin{array}{l}{\left( {x - 178} \right)^2} + {\left( {y - 430} \right)^2} \le 49\\0 \le z \le 43\end{array} \right.\).
Máy bay MiG-31 bay vào không phận bị hạn chế khi
\(\left\{ \begin{array}{l}{\left( {31 + 302t - 178} \right)^2} + {\left( {10 + 840t - 430} \right)^2} \le 49\\0 \le 11 + 64t \le 43\end{array} \right.\)\( \Leftrightarrow 0,4918 \le t \le \frac{1}{2}\).
Do đó, thời điểm máy bay MiG-31 bay ra khỏi khu vực không phận bị hạn chế là \(t = 0,5\) (giờ).
Khi đó, vị trí của hai máy bay Su-30 và MiG-31 là \(A\left( {246;395;42} \right)\) và \(B\left( {182;430;43} \right)\).
Khoảng cách giữa chúng là \(AB \approx 73\)(km).
Đáp án: 73.
Lời giải
a) Sai. Vectơ vận tốc là \(\overrightarrow v = \frac{{\overrightarrow {AB} }}{t} = \left( { - 4; - 1,5; - 0,5} \right)\).
b) Đúng. Đường thẳng \(AB\) đi qua \(A\left( {320;148;45} \right)\) và có vectơ chỉ phương \(\overrightarrow {AB} = \left( { - 40; - 15; - 5} \right)\)nên ta có phương trình đường thẳng là \(\left\{ \begin{array}{l}x = 320 - 40t\\y = 148 - 15t\\z = 45 - 5t\end{array} \right.\).
c) Đúng. Phương trình chuyển động tại thời điểm \(t\) giây là \(\left\{ \begin{array}{l}x = 320 - 4t\\y = 148 - 1,5t\\z = 45 - 0,5t\end{array} \right.\).
Vật chạm đất tức là \(z\left( t \right) = 0 \Leftrightarrow 45 - 0,5t = 0 \Leftrightarrow t = 90\).
d) Sai. Radar phát hiện khi \(r\left( t \right) = \sqrt {{{\left( {380 - 4t} \right)}^2} + {{\left( {148 - 1,5t} \right)}^2} + \left( {45 - 0,5{t^2}} \right)} = 400\).
Giải phương trình ta được \(t \approx 0,11\).
Khi đó cao độ của vật là \(z\left( {0,11} \right) = 45 - 0,5.0,11 = 44,945 \approx 44,95\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\[4x + 3y + 7z - 11 = 0\].
\[4x + 3y + 7z + 11 = 0\].
\[4x + 3y - 7z + 11 = 0\].
\[4x + 3y - 7z - 11 = 0\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\(M\left( {3;4; - 5} \right)\).
\(N\left( {2; - 5;3} \right)\).
\(P\left( { - 3; - 4;5} \right)\).
\(Q\left( {2;5; - 3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.