Một nhà máy tuyển kỹ sư làm việc trong thời hạn 5 năm với mức lương năm đầu là 220 triệu đồng và cam kết sẽ tăng thêm 5% lương mỗi năm so với năm liền trước đó. Tính tổng số tiền lương mà kỹ sư nhận được sau 4 năm làm việc.
Một nhà máy tuyển kỹ sư làm việc trong thời hạn 5 năm với mức lương năm đầu là 220 triệu đồng và cam kết sẽ tăng thêm 5% lương mỗi năm so với năm liền trước đó. Tính tổng số tiền lương mà kỹ sư nhận được sau 4 năm làm việc.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Mức lương năm thứ hai kỹ sư nhận được là \(220 + 220.5\% = 220.\left( {1 + 5\% } \right)\) triệu đồng.
Mức lương năm thứ ba kỹ sư nhận được là \(220\left( {1 + 5\% } \right) + 220\left( {1 + 5\% } \right).5\% = 220.{\left( {1 + 5\% } \right)^2}\) triệu đồng.
Mức lương năm thứ tư kỹ sư nhân được là \(220.{\left( {1 + 5\% } \right)^3}\) triệu đồng.
Tổng số tiền lương mà kỹ sư nhận được sau 4 năm làm việc là:
\(220 + 220.\left( {1 + 5\% } \right) + 220.{\left( {1 + 5\% } \right)^2} + 220.{\left( {1 + 5\% } \right)^3} = 220.\frac{{1 - {{\left( {1 + 5\% } \right)}^4}}}{{1 - \left( {1 + 5\% } \right)}} \approx 948\) triệu đồng.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
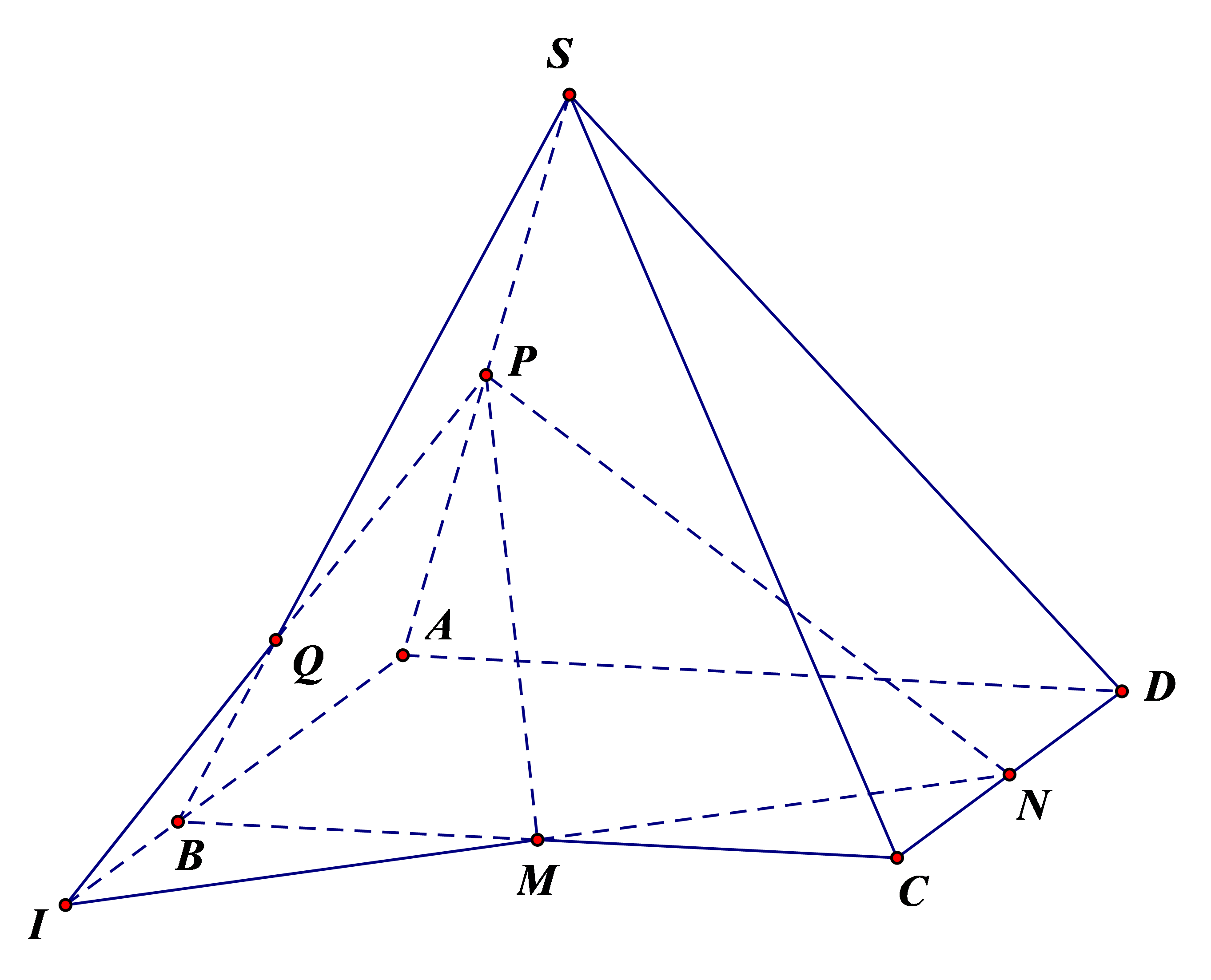
Trong mặt phẳng \(\left( {ABCD} \right)\) có \(I = MN \cap AB\).
Trong mặt phẳng \(\left( {SAB} \right)\) có \(Q = IP \cap SB\) mà \(IP \subset \left( {MNP} \right)\). Do đó \(Q = SB \cap \left( {MNP} \right)\).
Có \(IB//CN\) nên \(\frac{{IB}}{{CN}} = \frac{{MB}}{{MC}} = 1\) \( \Rightarrow \frac{{IB}}{{IA}} = \frac{1}{3}\).
Áp dụng định lí Menelaus cho \(\Delta SAB\) có \(\frac{{SP}}{{PA}}.\frac{{AI}}{{IB}}.\frac{{BQ}}{{QS}} = 1\)\( \Leftrightarrow 1.3.\frac{{BQ}}{{QS}} = 1\)\( \Rightarrow \frac{{BQ}}{{QS}} = \frac{1}{3}\).
Câu 2
A. Ba điểm không thẳng hàng mà nó đi qua.
B. Hai điểm thuộc mặt phẳng.
C. Một đường thẳng và một điểm thuộc nó.
D. Ba điểm mà nó đi qua.
Lời giải
Một mặt phẳng hoàn toàn được xác định nếu đi qua ba điểm không thẳng hàng. Chọn A.
Câu 3
A. \(10\).
B. \(6\).
C. \( - 16\).
D. \( - 10\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right) = \frac{{3x + 1}}{{x - 1}}\). Khi đó
a) \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \).
b) \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 4\).
c) Hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0} = 1\).
d) Hàm số \(y = f\left( x \right)\) liên tục trên từng khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right) = \frac{{3x + 1}}{{x - 1}}\). Khi đó
a) \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \).
b) \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 4\).
c) Hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0} = 1\).
d) Hàm số \(y = f\left( x \right)\) liên tục trên từng khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập