Cho tứ diện đều \(ABCD\) cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(CD\), \(G\) là trung điểm của \(AM\) biết \(\overrightarrow {BG} .\overrightarrow {AC} = n{a^2}\) ( \(n\) là số thập phân). Tìm \(n\) (kết quả làm tròn đến hàng phần mười).
Quảng cáo
Trả lời:
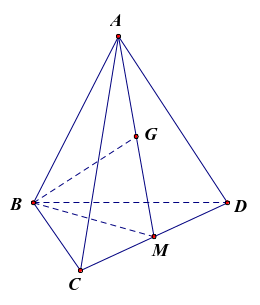
Ta có \(\overrightarrow {BG} .\overrightarrow {AC} = \left( {\overrightarrow {AG} - \overrightarrow {AB} } \right).\overrightarrow {AC} = \overrightarrow {AG} .\overrightarrow {AC} - \overrightarrow {AB} .\overrightarrow {AC} \)\( = \left| {\overrightarrow {AG} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AG} ,\overrightarrow {AC} } \right) - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)
\( = \frac{1}{2}\left| {\overrightarrow {AM} } \right|.\left| {\overrightarrow {AC} } \right|.\cos 30^\circ - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos 60^\circ \)\( = \frac{1}{2}.\frac{{a\sqrt 3 }}{2}.a.\frac{{\sqrt 3 }}{2} - a.a.\frac{1}{2} = - \frac{1}{8}{a^2}\).
Suy ra \(n = - 0,1\).
Trả lời: −0,1.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Giả sử sau 5 giây cabin di chuyển đến điểm \(M\left( {x;y;z} \right)\).
Khi đó ta có \(\overrightarrow {AM} \) và \(\overrightarrow u \) cùng hướng suy ra \(\overrightarrow {AM} = t\overrightarrow u = \left( {t;2t; - 2t} \right)\left( {t > 0} \right)\).
Mà quãng đường cabin đi được trong 5 giây là \(6.5 = 30\)(m).
Do đó \(AM = 30 \Leftrightarrow A{M^2} = 900 \Leftrightarrow {t^2} + 4{t^2} + 4{t^2} = 900 \Rightarrow t = 10\).
Suy ra \(\overrightarrow {AM} = \left( {10;20; - 20} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}x + 1 = 10\\y - 4 = 20\\z - 3 = - 20\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 9\\y = 24\\z = - 17\end{array} \right.\) \( \Rightarrow M\left( {9;24; - 17} \right)\).
Khi đó khoảng cách giữa cabin và người quan sát là \(BM = \sqrt {{{\left( {9 - 2} \right)}^2} + {{\left( {24 - 0} \right)}^2} + {{\left( { - 17 + 1} \right)}^2}} = \sqrt {881} \) m.
Lời giải
Gọi \(I\) là trọng tâm của tam giác \(ABC\).
Khi đó \(I\left( {1;1; - 1} \right)\) và \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \).
Khi đó \(f = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| + 3\left| {\overrightarrow {MD} } \right|\)\( = \left| {3\overrightarrow {MI} + \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} } \right| + 3\left| {\overrightarrow {MD} } \right| = 3\left( {\left| {\overrightarrow {MI} } \right| + \left| {\overrightarrow {MD} } \right|} \right)\).
Bài toán trở thành tìm \(M\left( {a;b;0} \right) \in \left( {Oxy} \right)\) sao cho \(f = 3\left( {\left| {\overrightarrow {MI} } \right| + \left| {\overrightarrow {MD} } \right|} \right)\) đạt giá trị nhỏ nhất.
Vì \({z_I}.{z_D} > 0\) nên điểm \(I\) và \(D\) nằm cùng phía với mặt phẳng \(\left( {Oxy} \right)\).
Gọi \(I'\left( {1;1;1} \right)\) là điểm đối xứng với \(I\) qua mặt phẳng \(\left( {Oxy} \right)\).
Khi đó \(f = 3\left( {\left| {\overrightarrow {MI} } \right| + \left| {\overrightarrow {MD} } \right|} \right) = 3\left( {\left| {\overrightarrow {MI'} } \right| + \left| {\overrightarrow {MD} } \right|} \right) \ge 3I'D\).
Để \(f\) nhỏ nhất thì \(I';M;D\) thẳng hàng suy ra \(\overrightarrow {I'M} \) và \(\overrightarrow {I'D} \) cùng hướng
\( \Leftrightarrow \frac{{a - 1}}{{ - 1}} = \frac{{b - 1}}{1} = \frac{{ - 1}}{{ - 3}}\)\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{2}{3}\\b = \frac{4}{3}\end{array} \right.\) \( \Rightarrow M\left( {\frac{2}{3};\frac{4}{3};0} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
\(\left( {4;1 + \sqrt 2 ; - 1} \right);\left( {4;1 - \sqrt 2 ; - 1} \right)\).
\(\left( {4;1; - 1} \right)\).
\[\left( {2;1; - 1} \right)\].
\(\left( {2; - 1; - 1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\(\overrightarrow {AD'} \).
\(\overrightarrow {AB'} \).
\(\overrightarrow {AC'} \).
\(\overrightarrow {AC} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\(\left( { - \infty ;1} \right)\).
\(\left( { - \infty ; - 1} \right)\).
\[\left( {1;3} \right)\].
\(\left( {3; + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.