Cho đường tròn \[\left( O \right)\] bán kính \[OA.\] Từ trung điểm \[M\] của \[OA\] vẽ dây \[BC \bot OA.\] Biết độ dài đường tròn \[\left( O \right)\] là \[4\pi {\rm{\;cm}}.\] Độ dài cung lớn \[BC\] bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm)
Cho đường tròn \[\left( O \right)\] bán kính \[OA.\] Từ trung điểm \[M\] của \[OA\] vẽ dây \[BC \bot OA.\] Biết độ dài đường tròn \[\left( O \right)\] là \[4\pi {\rm{\;cm}}.\] Độ dài cung lớn \[BC\] bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm)
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án: 8,38
|
Ta có \(BC \bot OA\) tại trung điểm \[M\] của \[OA\] nên \(BC\) là đường trung trực của đoạn thẳng \(OA.\) Do đó \[OB = AB.\] Mà \[OA = OB\] nên \[OA = OB = AB.\] Suy ra tam giác \[OAB\] là tam giác đều. Do đó \[\widehat {AOB} = 60^\circ .\] Chứng minh tương tự, ta được \[\widehat {AOC} = 60^\circ .\] Ta có Khi đó số đo cung lớn \[BC\] bằng Độ dài cung lớn \[BC\] là: \[l = \frac{n}{{360}}C = \frac{{240}}{{360}} \cdot 4\pi = \frac{{8\pi }}{3}{\rm{\;}}\left( {{\rm{cm}}} \right) \approx 8,38{\rm{ cm}}{\rm{.}}\] |
|
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đúng. b) Sai. c) Sai. d) Đúng.
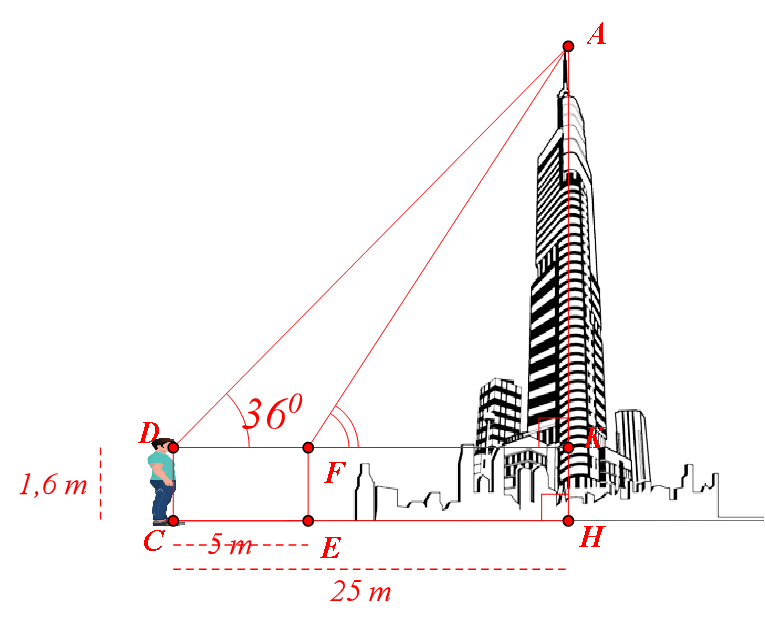
• Xét \[\Delta AKD\] vuông tại \[D\], ta có: \[\tan 36^\circ = \tan D = \frac{{AK}}{{KD}}\] hay \[AK = AD \cdot \tan 36^\circ \].
Do đó, ý a) là đúng.
• Ta có: \[FK = EH = CH - CE = 25 - 5 = 20{\rm{\;(m)}}{\rm{.}}\]
Do đó, ý b) là đúng.
• Từ \[\tan 36^\circ = \tan D = \frac{{AK}}{{KD}},\] ta có \[AK = KD \cdot \tan 36^\circ = 25 \cdot \tan 36^\circ \approx 18,164{\rm{\;(m)}}{\rm{.}}\]
Ta có \[AH = AK + KH \approx 18,164 + 1,6 = 19,764 \approx 20{\rm{\;(m)}}{\rm{.}}\]
Vậy độ dài tòa nhà chính là độ dài đoạn \[AH\] và khoảng 20 m.
Do đó, ý c) là sai.
• Xét \[\Delta AFK\] vuông tại \[K\], ta có: \[\tan F = \frac{{AK}}{{KF}} \approx \frac{{18,164}}{{20}}\], do đó \[\widehat {KFA} \approx 42^\circ .\]
Vậy góc nâng từ \[F\] đến nóc tòa nhà khoảng \[42^\circ \].
Vậy ý d) là đúng.
Lời giải
Hướng dẫn giải
![ho nửa đường tròn tâm \[O\] đư (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/37-1761145264.png)
a) Có \[AP\] là tiếp tuyến của đường tròn \[\left( O \right)\] tại \[A\] nên \[AP \bot AO\].
\[MP\] là tiếp tuyến của đường tròn \[\left( O \right)\] tại \[M\] nên \[PM \bot MO\].
Tam giác \[APO\] vuông tại \[A\] nên ba điểm \[A,\,P,\,O\] cùng thuộc đường tròn đường kính \[PO\]. (1)
Tam giác \[POM\] vuông tại \[M\] nên ba điểm \[M,\,P,\,O\] cùng thuộc đường tròn đường kính \[PO\]. (2)
Từ (1) và (2) suy ra bốn điểm \[A,\,P,\,M,\,O\] cùng thuộc một đường tròn đường kính \[PO\].
b) Trong \[\left( O \right)\] có tam giác \[AMB\] có \[OA = OB = OM = \frac{1}{2}AB\] nên tam giác \[AMB\] vuông tại \[M\].
Do đó, \[\widehat {AMB} = 90^\circ \] hay \[AM \bot MB.\] (*)
Mà xét \[\Delta PAO\] và \[\Delta PMO\] có: \[AO = OM = R\] và \[PO\] chung.
Do đó, \[\Delta PAO = \Delta PMO\] (ch – cgv).
Suy ra \[PA = PM\] và \[AO = AM\] (hai cạnh tương ứng)
Do đó, \[PO\] là đường trung trực của \[AM\].
Suy ra \[AM \bot PO\]. (**)
Từ (*) và (**), có \[PO\parallel NB\] nên \[\widehat {AOP} = \widehat {OBN}\] (so le trong)
Xét \[\Delta PAO\] và \[\Delta NOB\] có:
\[AO = OB = R\] (gt)
\[\widehat {PAO} = \widehat {OBN}\] (so le trong)
Do đó, \[\Delta PAO = \Delta NOB\] (cgv – gn)
Suy ra \[PO = NB\] (hai cạnh tương ứng)
Xét tứ giác \[OBNP\] có: \[PO = NB\] và \[PO\parallel NB\] nên \[OBNP\] là hình bình hành.
Suy ra \[PN\parallel OB\].
Mà \[ON \bot OB\] nên \[ON \bot PN\] do đó \[\widehat {PNO} = 90^\circ \].
Có \[\Delta MOA\] cân tại \[O\] (vì \[OA = OM\]) nên \[\widehat {OAM} = \widehat {AMO}\] (3).
Có \[\widehat {AMO} = \widehat {PMN}\] (cùng phụ với \[\widehat {AMP}\]) (4)
Và \[\widehat {MAO} = \widehat {PON}\] (cùng phụ với \[\widehat {POA}\]) (5)
Từ (3), (4), (5) suy ra \[\widehat {PMN} = \widehat {PON}\].
Mà \[\widehat {PMN} = \widehat {MPO}\] (vì \[MN\parallel PO\])
Suy ra \[\widehat {OPM} = \widehat {PON}\] hay \[\widehat {POI} = \widehat {IPO}\].
Vậy \[\Delta OPI\] cân tại \[I.\]
c) Xét tứ giác \[APNO\] có \[\widehat {PAO} = \widehat {AON} = \widehat {PNO} = 90^\circ \]
Suy ra \[APNO\] là hình chữ nhật.
Mà \[PO \cap AN = K\] nên \[K\] là trung điểm của \[PO.\]
Xét \[\Delta POI\] cân tại \[I:\] có \[K\] là trung điểm \[PO\] nên \[IK\] là đường trung tuyến đồng thời là đường cao.
Do đó, \[IK \bot PO.\]
Xét \[\Delta JPO\] có \[ON \bot PJ,\,\,PM \bot OJ,\,\,ON \cap PM = I\] nên \[I\] là trực tâm của \[\Delta JPO\].
Suy ra \[IJ \bot PO\].
Từ đây suy ra \[I,\,J,\,K\] thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho đường tròn \[\left( O \right)\] bán kính \[OA.\] Từ trung điểm \[M\] của \[OA\] vẽ dây \[BC \bot OA.\] Biết độ dài đường tròn \[\left( O \right)\] là \[4\pi {\rm{\;cm}}.\] Độ dài cung lớn \[BC\] bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/22-1761105129.png)