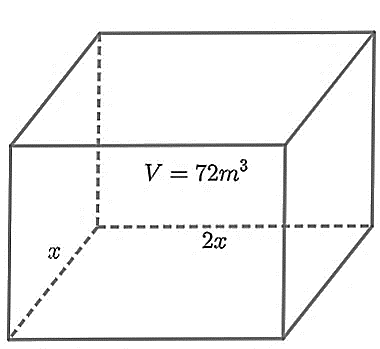
(0,5 điểm) Bác Sơn muốn xây một bể chứa nước có dạng hình hộp chữ nhật không nắp có thể tích bằng \(72{\rm{ }}{{\rm{m}}^3}\). Đáy bể có dạng hình chữ nhật với chiều rộng là \(x{\rm{ }}\left( {\rm{m}} \right)\), chiều dài gấp đôi chiều rộng. Bác Sơn muốn phần diện tích cần xây (bao gồm diện tích xung quanh và diện tích đáy bể) là nhỏ nhất để tiết kiệm chi phí thì \(x\) phải bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?

Quảng cáo
Trả lời:
Hướng dẫn giải
Chiều dài của đáy bể là \(2x{\rm{\;(m)}}{\rm{.}}\)
Diện tích đáy của bể là \(2{x^2}{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right).\)
Chiều cao của bể là: \(\frac{{72}}{{2{x^2}}} = \frac{{36}}{{{x^2}}}{\rm{ }}\left( {\rm{m}} \right)\).
Diện tích xung quanh của bể là: \(2 \cdot \frac{{36}}{{{x^2}}} \cdot \left( {x + 2x} \right) = \frac{{72 \cdot 3x}}{{{x^2}}} = \frac{{216}}{x}{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
Diện tích cần xây bằng tổng diện tích xung quanh và diện tích đáy của bể, và bằng:
\(\frac{{216}}{x}{\rm{ + }}2{x^2}{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
Do \(x\) là chiều rộng của bể nên \(x > 0\), áp dụng bất đẳng thức Cauchy, ta có:
\(2{x^2} + \frac{{216}}{x} = 2{x^2} + \frac{{108}}{x} + \frac{{108}}{x} \ge 3\sqrt[3]{{2{x^2} \cdot \frac{{108}}{x} \cdot \frac{{108}}{x}}}{\rm{ }}\)
Suy ra \(2{x^2} + \frac{{216}}{x} \ge 3\sqrt[3]{{23\,\,328}} \approx 85,72\)
Dấu “=” xảy ra khi \(2{x^2} = \frac{{108}}{x} = \frac{{108}}{x}\) hay \(2{x^3} = 108\), tức là \(x = \sqrt[3]{{54}} \approx 3,78{\rm{ m}}{\rm{.}}\)
Vậy muốn diện tích cần xây là tiết kiệm chi phí nhất thì \(x \approx 3,78{\rm{ m}}{\rm{.}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đúng. b) Sai. c) Sai. d) Đúng.
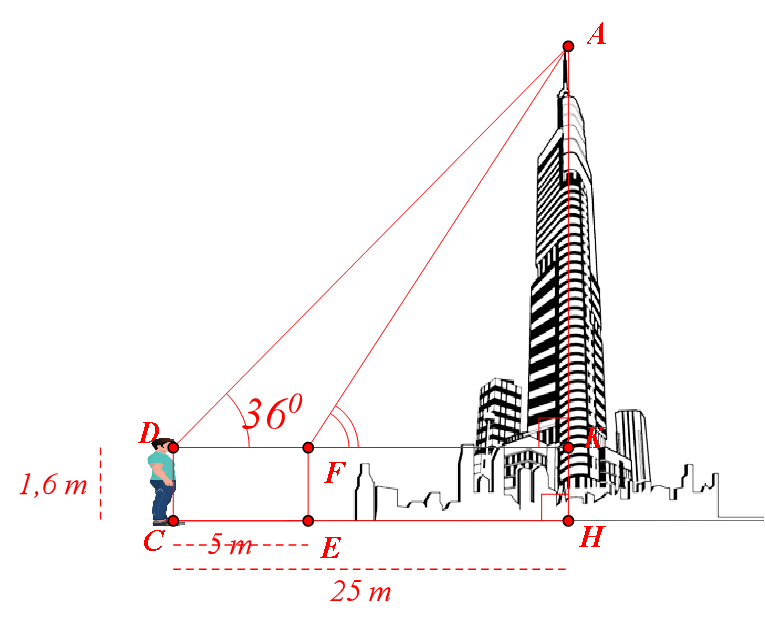
• Xét \[\Delta AKD\] vuông tại \[D\], ta có: \[\tan 36^\circ = \tan D = \frac{{AK}}{{KD}}\] hay \[AK = AD \cdot \tan 36^\circ \].
Do đó, ý a) là đúng.
• Ta có: \[FK = EH = CH - CE = 25 - 5 = 20{\rm{\;(m)}}{\rm{.}}\]
Do đó, ý b) là đúng.
• Từ \[\tan 36^\circ = \tan D = \frac{{AK}}{{KD}},\] ta có \[AK = KD \cdot \tan 36^\circ = 25 \cdot \tan 36^\circ \approx 18,164{\rm{\;(m)}}{\rm{.}}\]
Ta có \[AH = AK + KH \approx 18,164 + 1,6 = 19,764 \approx 20{\rm{\;(m)}}{\rm{.}}\]
Vậy độ dài tòa nhà chính là độ dài đoạn \[AH\] và khoảng 20 m.
Do đó, ý c) là sai.
• Xét \[\Delta AFK\] vuông tại \[K\], ta có: \[\tan F = \frac{{AK}}{{KF}} \approx \frac{{18,164}}{{20}}\], do đó \[\widehat {KFA} \approx 42^\circ .\]
Vậy góc nâng từ \[F\] đến nóc tòa nhà khoảng \[42^\circ \].
Vậy ý d) là đúng.
Lời giải
Hướng dẫn giải
![ho nửa đường tròn tâm \[O\] đư (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/37-1761145264.png)
a) Có \[AP\] là tiếp tuyến của đường tròn \[\left( O \right)\] tại \[A\] nên \[AP \bot AO\].
\[MP\] là tiếp tuyến của đường tròn \[\left( O \right)\] tại \[M\] nên \[PM \bot MO\].
Tam giác \[APO\] vuông tại \[A\] nên ba điểm \[A,\,P,\,O\] cùng thuộc đường tròn đường kính \[PO\]. (1)
Tam giác \[POM\] vuông tại \[M\] nên ba điểm \[M,\,P,\,O\] cùng thuộc đường tròn đường kính \[PO\]. (2)
Từ (1) và (2) suy ra bốn điểm \[A,\,P,\,M,\,O\] cùng thuộc một đường tròn đường kính \[PO\].
b) Trong \[\left( O \right)\] có tam giác \[AMB\] có \[OA = OB = OM = \frac{1}{2}AB\] nên tam giác \[AMB\] vuông tại \[M\].
Do đó, \[\widehat {AMB} = 90^\circ \] hay \[AM \bot MB.\] (*)
Mà xét \[\Delta PAO\] và \[\Delta PMO\] có: \[AO = OM = R\] và \[PO\] chung.
Do đó, \[\Delta PAO = \Delta PMO\] (ch – cgv).
Suy ra \[PA = PM\] và \[AO = AM\] (hai cạnh tương ứng)
Do đó, \[PO\] là đường trung trực của \[AM\].
Suy ra \[AM \bot PO\]. (**)
Từ (*) và (**), có \[PO\parallel NB\] nên \[\widehat {AOP} = \widehat {OBN}\] (so le trong)
Xét \[\Delta PAO\] và \[\Delta NOB\] có:
\[AO = OB = R\] (gt)
\[\widehat {PAO} = \widehat {OBN}\] (so le trong)
Do đó, \[\Delta PAO = \Delta NOB\] (cgv – gn)
Suy ra \[PO = NB\] (hai cạnh tương ứng)
Xét tứ giác \[OBNP\] có: \[PO = NB\] và \[PO\parallel NB\] nên \[OBNP\] là hình bình hành.
Suy ra \[PN\parallel OB\].
Mà \[ON \bot OB\] nên \[ON \bot PN\] do đó \[\widehat {PNO} = 90^\circ \].
Có \[\Delta MOA\] cân tại \[O\] (vì \[OA = OM\]) nên \[\widehat {OAM} = \widehat {AMO}\] (3).
Có \[\widehat {AMO} = \widehat {PMN}\] (cùng phụ với \[\widehat {AMP}\]) (4)
Và \[\widehat {MAO} = \widehat {PON}\] (cùng phụ với \[\widehat {POA}\]) (5)
Từ (3), (4), (5) suy ra \[\widehat {PMN} = \widehat {PON}\].
Mà \[\widehat {PMN} = \widehat {MPO}\] (vì \[MN\parallel PO\])
Suy ra \[\widehat {OPM} = \widehat {PON}\] hay \[\widehat {POI} = \widehat {IPO}\].
Vậy \[\Delta OPI\] cân tại \[I.\]
c) Xét tứ giác \[APNO\] có \[\widehat {PAO} = \widehat {AON} = \widehat {PNO} = 90^\circ \]
Suy ra \[APNO\] là hình chữ nhật.
Mà \[PO \cap AN = K\] nên \[K\] là trung điểm của \[PO.\]
Xét \[\Delta POI\] cân tại \[I:\] có \[K\] là trung điểm \[PO\] nên \[IK\] là đường trung tuyến đồng thời là đường cao.
Do đó, \[IK \bot PO.\]
Xét \[\Delta JPO\] có \[ON \bot PJ,\,\,PM \bot OJ,\,\,ON \cap PM = I\] nên \[I\] là trực tâm của \[\Delta JPO\].
Suy ra \[IJ \bot PO\].
Từ đây suy ra \[I,\,J,\,K\] thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.