Dạng 3. Trắc nghiệm trả lời ngắn

Trong mỗi câu hỏi, thí sinh viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

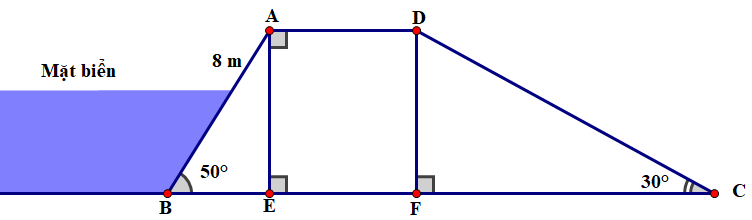
Một con đê được đắp chắn sóng theo hình dưới, biết \(\widehat {ABE} = 50^\circ ,\,\,\widehat {DCF} = 30^\circ \), độ dốc của con đê phía biển dài \(AB = 8\,\;{\rm{m}}{\rm{.}}\) Hỏi độ dốc còn lại \[CD\] của con đê dài bao nhiêu mét? (kết quả làm tròn đến chữ số thập phân thứ nhất).

Chọn C

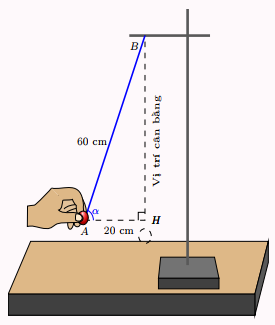
Gắn dữ kiện của bài toán vào mô hình Toán học như trên hình vẽ.

Gọi \[N\] là hình chiếu của \[M\] lên đoạn \[AH\].

Vì \[MN\] và \[BH\] là các đoạn thẳng nằm trên phương ngang; \[MB\] và \[NH\] nằm trên phương thẳng đứng nên tứ giác \[MBHN\] là hình chữ nhật.

Suy ra \[NH = MB = 1,55\,\,{\rm{m}}\]; \[MN = BH = 13,65\,\,{\rm{m}}\].

Tam giác \[ANM\] vuông tại \[N\] nên \[AN = MN \cdot \tan M.\]

Ta có:\[AH = AN + NH\]suy ra \[AH = MN \cdot \tan M + NH\].

Do đó \[AH = 13,65 \cdot \tan 58^\circ  + 1,55 \approx 23,39\,\,({\rm{m}}).\]

Vậy chiều cao của tháp khoảng \[23,39\,\,{\rm{m}}\].

Chọn C

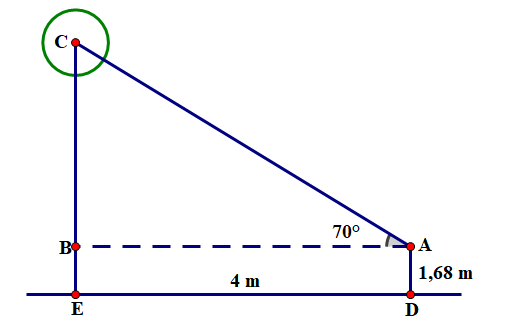
Gọi \(A,\,\,D\) là vị trí của người đứng;

\(C,\,\,D\) là vị trí bức tường phía trên và dưới cùng;

\[H\] là hình chiếu của \[A\] lên \[BC.\]

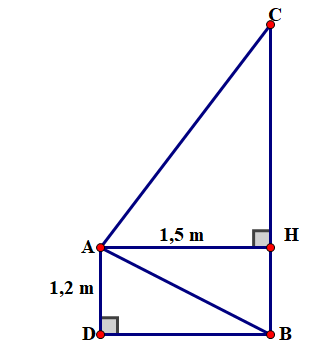
Tứ giác \[ADBH\] là hình chữ nhật nên \(BD = AH = 1,5\;\,{\rm{m}}\);

\[BH = AD = 1,2\;\,{\rm{m}}{\rm{.}}\]

Áp dụng định lí Pythagore vào tam giác \(ABD\) vuông tại \(D,\) ta có:

\(A{B^2} = A{D^2} + B{D^2} = 1,{2^2} + 1,{5^2} = 3,69\).

Suy ra \(AB = \sqrt {3,69}  = 1,92\;\,({\rm{m}}).\)

Xét \(\Delta ABC\) vuông tại \[A,\] đường cao \[AH,\] ta có:

\(A{B^2} = BH \cdot BC\) hay \(BC = \frac{{A{B^2}}}{{BH}} = \frac{{3,69}}{{1,2}} \approx 3\;\,\,({\rm{m}})\).

Vậy chiều cao của bức tường là \[3{\rm{ m}}.\]