Đề kiểm tra Toán 9 Cánh diều Chương 4 có đáp án - Đề 1
45 người thi tuần này 4.6 582 lượt thi 11 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề KSCL Toán 9 tháng 10 năm 2026-2027 Trường THCS Từ Liêm 1 (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 10 năm 2026-2027 Trường THCS Kim Giang (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 9 năm 2026-2027 Xã Đại Thanh (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Hồng Vân (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Ngô Sĩ Liên (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Yên Hòa (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Giảng Võ (Hà Nội) có đáp án
Danh sách câu hỏi:
Câu 1/11
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn D
Theo định nghĩa tỉ số lượng giác trong tam giác vuông: Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha ,\) kí hiệu cot \(\alpha .\)
Do đó, khẳng định D sai.
Câu 2/11
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn B
Đặt \[BN = x\,\,({\rm{cm)}}\,\,\,\left( {0 < x < 11} \right)\] Khi đó \[NC = 11 - x\,\,({\rm{cm)}}{\rm{.}}\]
Xét tam giác \(ABN\) vuông tại \(N\) có \(AN = BN \cdot \tan B = x \cdot \tan 40^\circ \).
Xét tam giác \(ACN\) vuông tại \(N\) có \(AN = CN \cdot \tan C = \left( {11 - x} \right)\tan 30^\circ \).
Suy ra \[x\tan 40^\circ = \left( {11 - x} \right)\tan 30^\circ \] nên \[x \approx 4,48\,\,{\rm{cm}}\] (thoả mãn).
Khi đó \(AN = BN \cdot \tan B = 4,48 \cdot \tan 40^\circ \approx 3,76\,\,({\rm{cm)}}\).
Câu 3/11
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
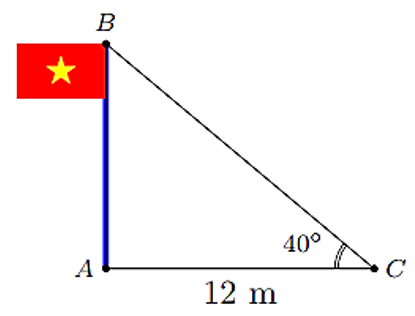
Xét tam giác \(ABC\) vuông tại \(A\), ta có:
\[AB = AC \cdot \tan \widehat C = 12\tan 40^\circ \approx 10,07\,\,({\mathop{\rm m}\nolimits} ).\]
Vậy chiều cao cột cờ \(AB\) khoảng \(10,07\,\,{\mathop{\rm m}\nolimits} .\)
Câu 4/11
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn B
Kẻ đường cao \(AH.\)
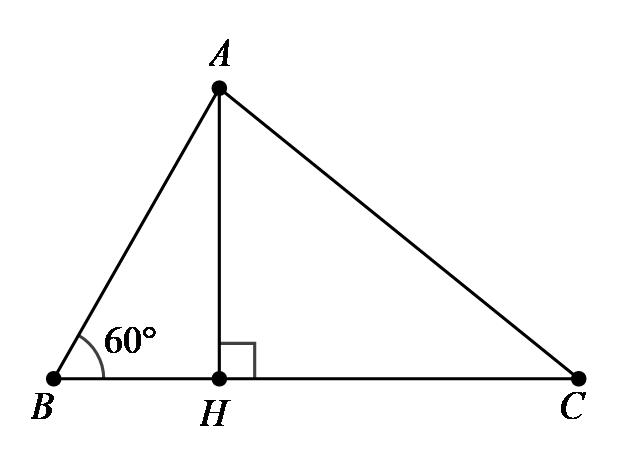
Xét tam giác vuông \(ABH\), ta có:
\[BH = AB \cdot \cos B = AB \cdot \cos 60^\circ = 12 \cdot \frac{1}{2} = 6\,\,({\rm{cm)}}{\rm{.}}\]
\(AH = AB \cdot \sin B = AB \cdot \sin 60^\circ = 12 \cdot \frac{{\sqrt 3 }}{2} = 6\sqrt 3 \,\,({\rm{cm)}}.\)
Áp dụng định lí Pythagore vào tam giác vuông \(AHC\), ta có: \(H{C^2} = A{C^2} - A{H^2} = {15^2} - {\left( {6\sqrt 3 } \right)^2} = 117\).
Suy ra \(HC = 3\sqrt {13} \,\,({\rm{cm)}}\).
Vậy \(BC = CH + HB = 3\sqrt {13} + 6\,\,({\rm{cm)}}\).
Câu 5/11
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn C
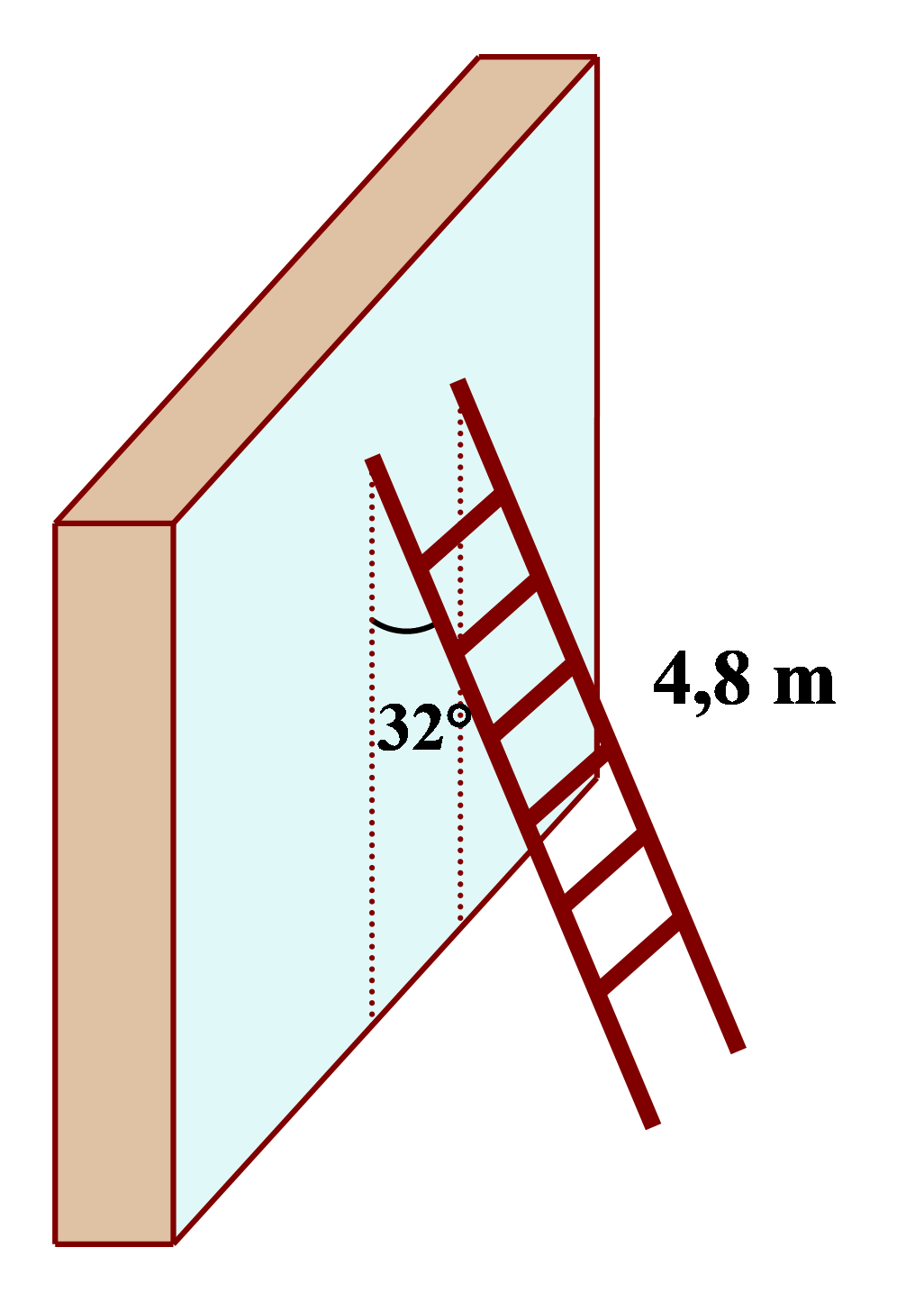
Gắn dữ kiện của bài toán vào mô hình Toán học như trên hình vẽ.
Xét \[\Delta AHB\] vuông tại \[H\], áp dụng hệ thức giữa cạnh và góc nhọn trong tam giác vuông ta có:
\[BH = AB \cdot \cos \widehat {HBA} = 4,8 \cdot \,\cos 32^\circ \approx 4,1\,\,{\rm{(m)}}{\rm{.}}\]
Vậy chiều cao của thang so với mặt đất là \[{\rm{4,1}}\,\,{\rm{m}}\].
Câu 6/11
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn A
Độ dài thang máy từ \[1\] lên tâng \[2\] là đoạn \[AB\].
Xét \[\Delta AHB\] vuông tại \[H\] có: \[\sin B = \frac{{AH}}{{AB}}\] hay \[AB = \frac{{AH}}{{\sin B}} = \frac{{4,2}}{{\sin 35^\circ }}\,\,({\rm{m}}).\]
Vì thang máy có tốc độ truyền là \[0,65\,\,{\rm{m/s}}\] nên thời gian để một người di chuyển từ tầng \[1\] lên tầng \[2\] bằng thang cuốn là: \[\frac{{AB}}{{0,65}} = \frac{{4,2}}{{0,65 \cdot \sin 35^\circ }} \approx 11,3\] (giây).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
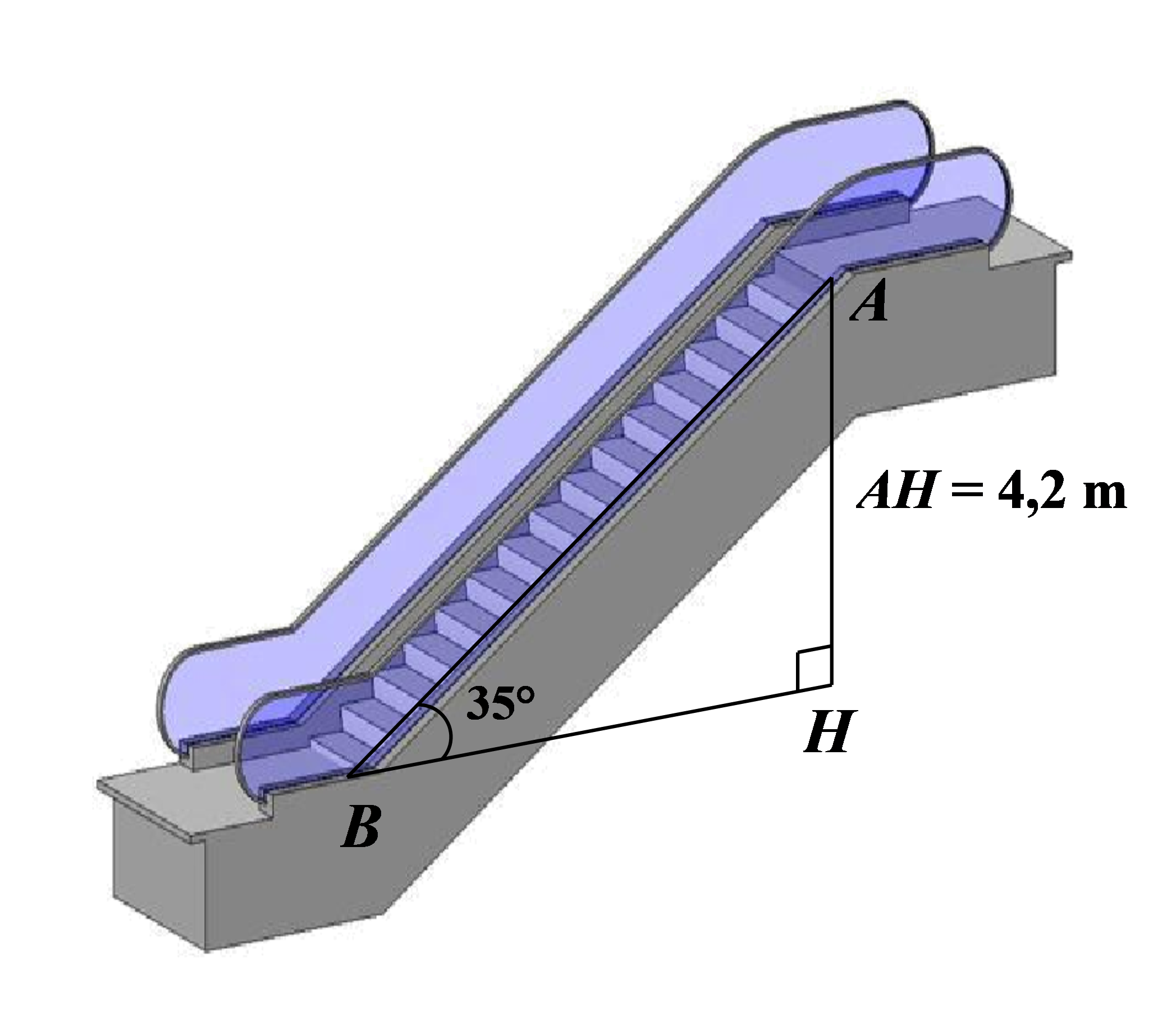
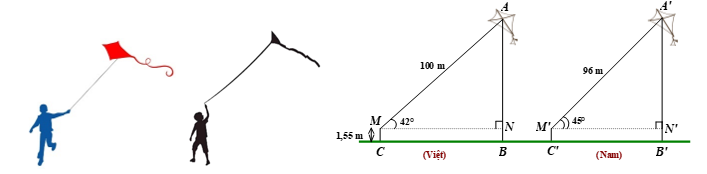
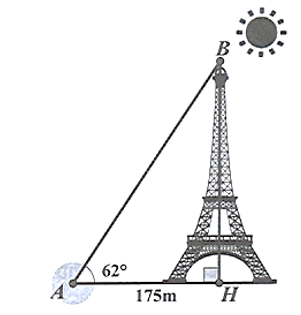
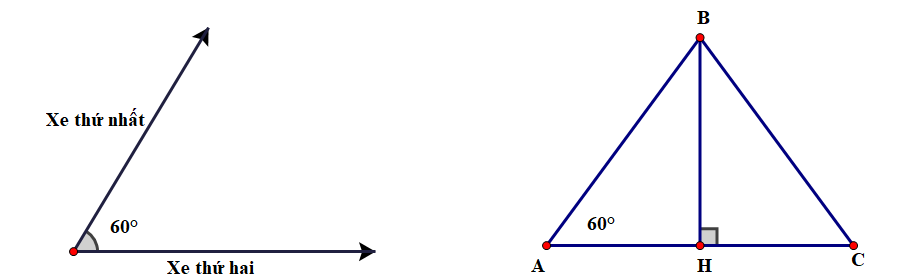
![núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\] Đáp án: 1906. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/62-1761201093.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 5/11 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập