Để phục vụ việc di chuyển của khách hàng giữa các tầng hàng trong siêu thị, người chủ đầu tư thường cho lắp hệ thống thang cuốn tự động. Biết rằng thang cuốn có góc nghiêng là \[35^\circ \] so với phương ngang và tốc độ truyền là \[0,65\,\,{\rm{m/s}}\], khoảng cách giữa hai tầng liên tiếp là \[4,2\,\,{\rm{m}}\]. Hỏi một người khi bước vào thang cuốn và đứng yên thì cần khoảng bao nhiêu giây để có thể di chuyển từ tầng \[1\] lên tầng \[2\]?
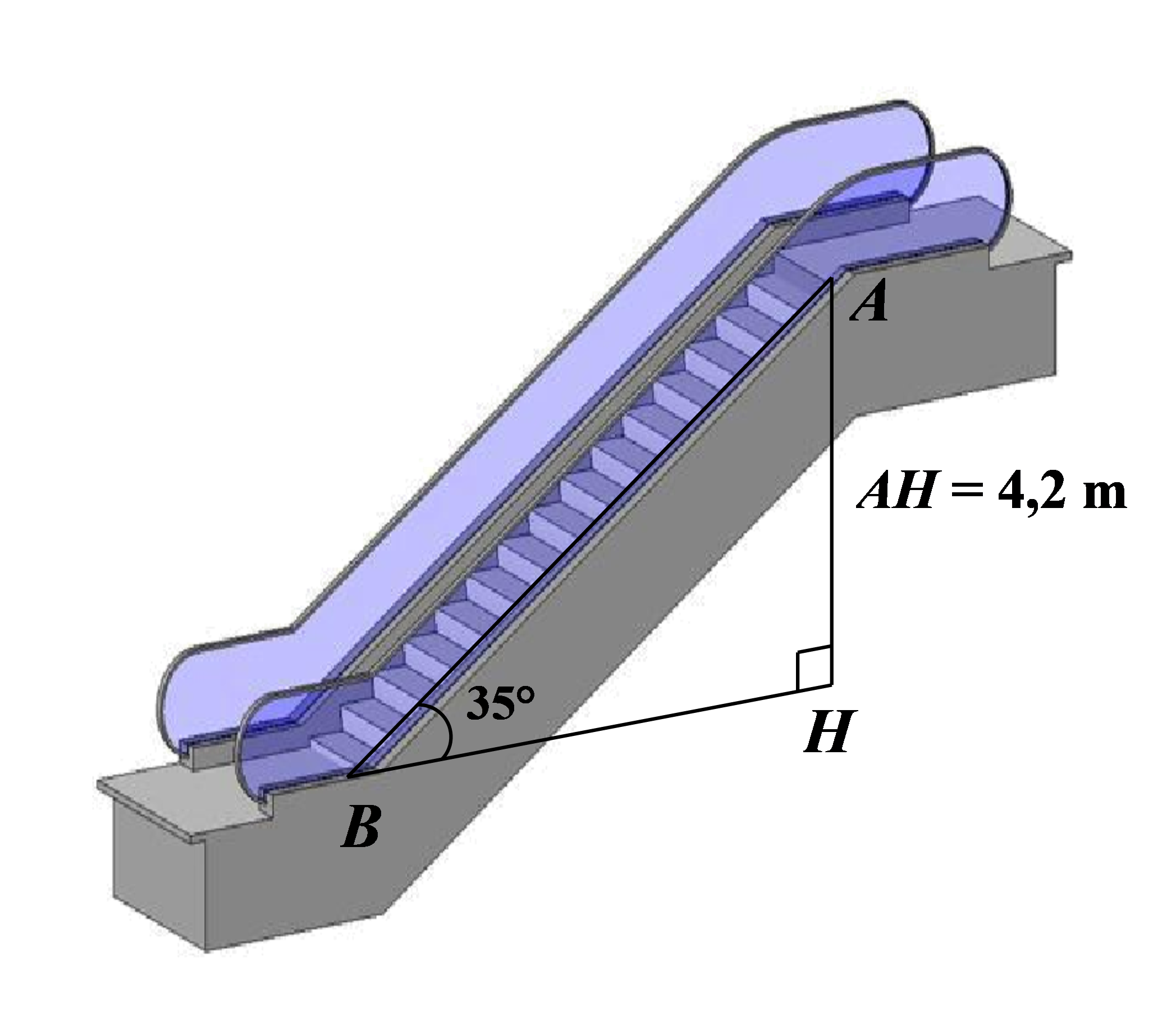
Để phục vụ việc di chuyển của khách hàng giữa các tầng hàng trong siêu thị, người chủ đầu tư thường cho lắp hệ thống thang cuốn tự động. Biết rằng thang cuốn có góc nghiêng là \[35^\circ \] so với phương ngang và tốc độ truyền là \[0,65\,\,{\rm{m/s}}\], khoảng cách giữa hai tầng liên tiếp là \[4,2\,\,{\rm{m}}\]. Hỏi một người khi bước vào thang cuốn và đứng yên thì cần khoảng bao nhiêu giây để có thể di chuyển từ tầng \[1\] lên tầng \[2\]?
Câu hỏi trong đề: Đề kiểm tra Toán 9 Cánh diều Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A
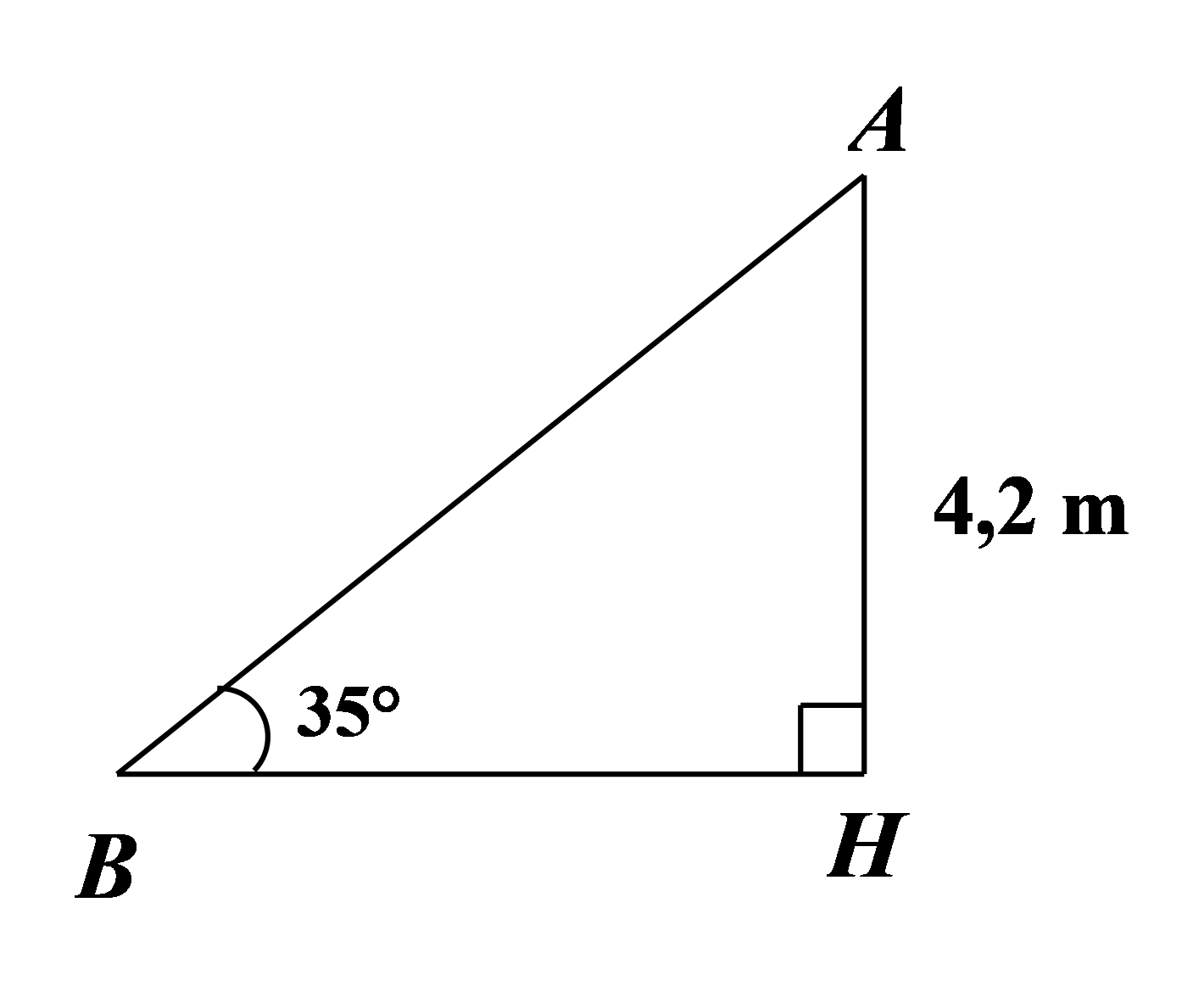
Độ dài thang máy từ \[1\] lên tâng \[2\] là đoạn \[AB\].
Xét \[\Delta AHB\] vuông tại \[H\] có: \[\sin B = \frac{{AH}}{{AB}}\] hay \[AB = \frac{{AH}}{{\sin B}} = \frac{{4,2}}{{\sin 35^\circ }}\,\,({\rm{m}}).\]
Vì thang máy có tốc độ truyền là \[0,65\,\,{\rm{m/s}}\] nên thời gian để một người di chuyển từ tầng \[1\] lên tầng \[2\] bằng thang cuốn là: \[\frac{{AB}}{{0,65}} = \frac{{4,2}}{{0,65 \cdot \sin 35^\circ }} \approx 11,3\] (giây).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
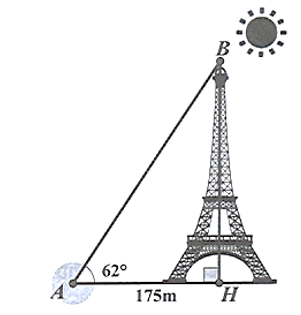
Xét \(\Delta ABH\) vuông tại \(H\), ta có:
\(\tan A = \frac{{BH}}{{AH}}\) hay \(\tan 62^\circ = \frac{{BH}}{{175}}\) nên \(BH = 175 \cdot \tan 62^\circ = 329\;\,({\rm{m}})\).
Vậy chiều cao của tháp Eiffel là \(329\;\,{\rm{m}}.\)
Đáp án: 329.
![núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\] Đáp án: 1906. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/62-1761201093.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
![núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\] Đáp án: 1906. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/10/63-1761201081.png)
Gọi \[D\] và \[E\] lần lượt là điểm đặt mắt khi người quan sát đỉnh núi đứng ở vị trí \[B\] và \[C.\]
Gọi \[I\] là hình chiếu của điểm \[D\] trên \[AH\].
So với mặt đất thì \[BD\] và \[CE\] là phương thẳng đứng; \[HC\] và \[IE\] là phương ngang nên các tứ giác \[IHBD,\,\,IHCE,\,\,DBCE\] là hình chữ nhật.
Do đó \[DE = BC = \,475\,\,{\rm{m}}\]; \[IH = DB = EC = 1,6\,\,{\rm{m}}\].
• Xét \[\Delta AID\] vuông tại \[I\] nên:
\[ID = AI \cdot \,\cot \widehat {ADI} = AI \cdot \,\cot 34^\circ = AI \cdot \tan 56^\circ \] (do \[\cot 34^\circ = \tan 56^\circ \]). \[\left( 1 \right)\]
• Xét \[\Delta AIE\] vuông tại \[I\] nên:
\[IE = AI \cdot \,\cot \widehat {AEI} = AI \cdot \,\cot 30^\circ = AI \cdot \tan 60^\circ \] (do \[\cot 30^\circ = \tan 60^\circ \]). \[\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[IE - ID = AI\left( {\tan 60^\circ - \tan 56^\circ } \right)\]
\[AI\left( {\tan 60^\circ - \tan 56^\circ } \right) = 475\]
\[AI = \frac{{475}}{{\tan 60^\circ - \tan 56^\circ }} \approx 1\,\,903,9\,\,({\rm{m}}).\]
Chiều cao \[AH\] của ngọn núi là:
\[AH = AI + IH \approx 1903,9\, + 1,6\, \approx 1906\,\,({\rm{m)}}{\rm{.}}\]
Vậy chiều cao \[AH\] của ngọn núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\]
Đáp án: 1906.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập