Để xác định chiều cao \[AH\] của một ngọn núi, người quan sát đứng từ hai vị trí \[B\] và \[C\] cách nhau \[475\,\,{\rm{m}}\] trên mặt đất. Tại vị trí \[B\], người đó quan sát đỉnh núi với phương nhìn tạo với phương nằm ngang một góc bằng \[34^\circ \]; tại vị trí \[C\], người đó quan sát đỉnh núi với phương nhìn tạo với phương nằm ngang một góc bằng \[30^\circ \] (hình vẽ). Biết rằng tầm mắt của người quan sát là \[{\rm{1,6}}\,\,{\rm{m}}\] và giả thiết ba điểm \[H,\,\,B,\,\,C\] thẳng hàng. Tính chiều cao của ngọn núi (đơn vị mét, kết quả làm tròn đến hàng đơn vị).
![núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\] Đáp án: 1906. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/62-1761201093.png)
Để xác định chiều cao \[AH\] của một ngọn núi, người quan sát đứng từ hai vị trí \[B\] và \[C\] cách nhau \[475\,\,{\rm{m}}\] trên mặt đất. Tại vị trí \[B\], người đó quan sát đỉnh núi với phương nhìn tạo với phương nằm ngang một góc bằng \[34^\circ \]; tại vị trí \[C\], người đó quan sát đỉnh núi với phương nhìn tạo với phương nằm ngang một góc bằng \[30^\circ \] (hình vẽ). Biết rằng tầm mắt của người quan sát là \[{\rm{1,6}}\,\,{\rm{m}}\] và giả thiết ba điểm \[H,\,\,B,\,\,C\] thẳng hàng. Tính chiều cao của ngọn núi (đơn vị mét, kết quả làm tròn đến hàng đơn vị).
![núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\] Đáp án: 1906. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/62-1761201093.png)
Câu hỏi trong đề: Đề kiểm tra Toán 9 Cánh diều Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
![núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\] Đáp án: 1906. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/10/63-1761201081.png)
Gọi \[D\] và \[E\] lần lượt là điểm đặt mắt khi người quan sát đỉnh núi đứng ở vị trí \[B\] và \[C.\]
Gọi \[I\] là hình chiếu của điểm \[D\] trên \[AH\].
So với mặt đất thì \[BD\] và \[CE\] là phương thẳng đứng; \[HC\] và \[IE\] là phương ngang nên các tứ giác \[IHBD,\,\,IHCE,\,\,DBCE\] là hình chữ nhật.
Do đó \[DE = BC = \,475\,\,{\rm{m}}\]; \[IH = DB = EC = 1,6\,\,{\rm{m}}\].
• Xét \[\Delta AID\] vuông tại \[I\] nên:
\[ID = AI \cdot \,\cot \widehat {ADI} = AI \cdot \,\cot 34^\circ = AI \cdot \tan 56^\circ \] (do \[\cot 34^\circ = \tan 56^\circ \]). \[\left( 1 \right)\]
• Xét \[\Delta AIE\] vuông tại \[I\] nên:
\[IE = AI \cdot \,\cot \widehat {AEI} = AI \cdot \,\cot 30^\circ = AI \cdot \tan 60^\circ \] (do \[\cot 30^\circ = \tan 60^\circ \]). \[\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[IE - ID = AI\left( {\tan 60^\circ - \tan 56^\circ } \right)\]
\[AI\left( {\tan 60^\circ - \tan 56^\circ } \right) = 475\]
\[AI = \frac{{475}}{{\tan 60^\circ - \tan 56^\circ }} \approx 1\,\,903,9\,\,({\rm{m}}).\]
Chiều cao \[AH\] của ngọn núi là:
\[AH = AI + IH \approx 1903,9\, + 1,6\, \approx 1906\,\,({\rm{m)}}{\rm{.}}\]
Vậy chiều cao \[AH\] của ngọn núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\]
Đáp án: 1906.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
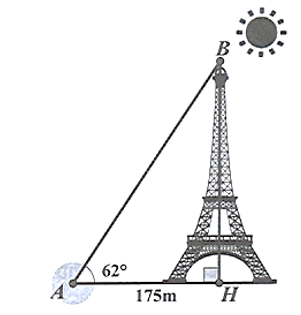
Xét \(\Delta ABH\) vuông tại \(H\), ta có:
\(\tan A = \frac{{BH}}{{AH}}\) hay \(\tan 62^\circ = \frac{{BH}}{{175}}\) nên \(BH = 175 \cdot \tan 62^\circ = 329\;\,({\rm{m}})\).
Vậy chiều cao của tháp Eiffel là \(329\;\,{\rm{m}}.\)
Đáp án: 329.
Câu 2
Lời giải
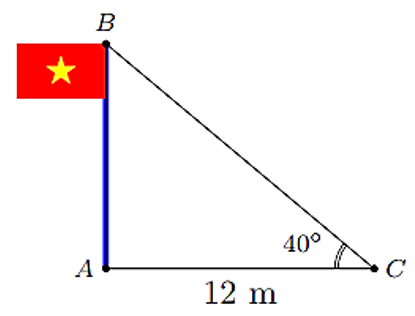
Xét tam giác \(ABC\) vuông tại \(A\), ta có:
\[AB = AC \cdot \tan \widehat C = 12\tan 40^\circ \approx 10,07\,\,({\mathop{\rm m}\nolimits} ).\]
Vậy chiều cao cột cờ \(AB\) khoảng \(10,07\,\,{\mathop{\rm m}\nolimits} .\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.