Phần 3. Trắc nghiệm trả lời ngắn
Trong mỗi câu hỏi, thí sinh viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
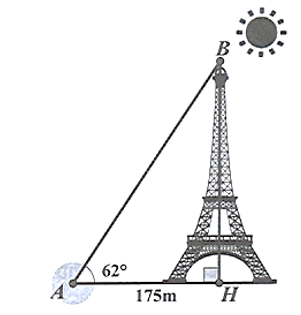
Tháp Eiffel là một công trình kiến trúc bằng thép nằm trên công viên Champ-de-Mars, cạnh sông Seinc, là biểu tượng của Thủ đô Paris nước Pháp. Công trình này do kỹ sư Gustave Eiffel và các đồng nghiệp của mình thiết kế, xây dựng từ năm 1887 đến năm 1889 nhân dịp Triển lãm thế giới năm 1889 và cũng là dịp kỷ niệm 100 năm Cách mạng Pháp.Hãy tính chiều cao của tháp Eiffel mà không cần lên đỉnh tháp, biết góc tạo bởi tia nắng mặt trời với mặt đất là \(62^\circ {\rm{C}}\) và bóng của tháp trên mặt đất là \[175{\rm{ m}}\] (đơn vị mét, làm tròn kết quả đến hàng đơn vị).
Phần 3. Trắc nghiệm trả lời ngắn
Trong mỗi câu hỏi, thí sinh viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tháp Eiffel là một công trình kiến trúc bằng thép nằm trên công viên Champ-de-Mars, cạnh sông Seinc, là biểu tượng của Thủ đô Paris nước Pháp. Công trình này do kỹ sư Gustave Eiffel và các đồng nghiệp của mình thiết kế, xây dựng từ năm 1887 đến năm 1889 nhân dịp Triển lãm thế giới năm 1889 và cũng là dịp kỷ niệm 100 năm Cách mạng Pháp.Hãy tính chiều cao của tháp Eiffel mà không cần lên đỉnh tháp, biết góc tạo bởi tia nắng mặt trời với mặt đất là \(62^\circ {\rm{C}}\) và bóng của tháp trên mặt đất là \[175{\rm{ m}}\] (đơn vị mét, làm tròn kết quả đến hàng đơn vị).
Câu hỏi trong đề: Đề kiểm tra Toán 9 Chân trời sáng tạo Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
Xét \(\Delta ABH\) vuông tại \(H\), ta có:
\(\tan A = \frac{{BH}}{{AH}}\) hay \(\tan 62^\circ = \frac{{BH}}{{175}}\) nên \(BH = 175 \cdot \tan 62^\circ = 329\;\,({\rm{m}})\).
Vậy chiều cao của tháp Eiffel là \(329\;\,{\rm{m}}.\)
Đáp án: 329.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn B
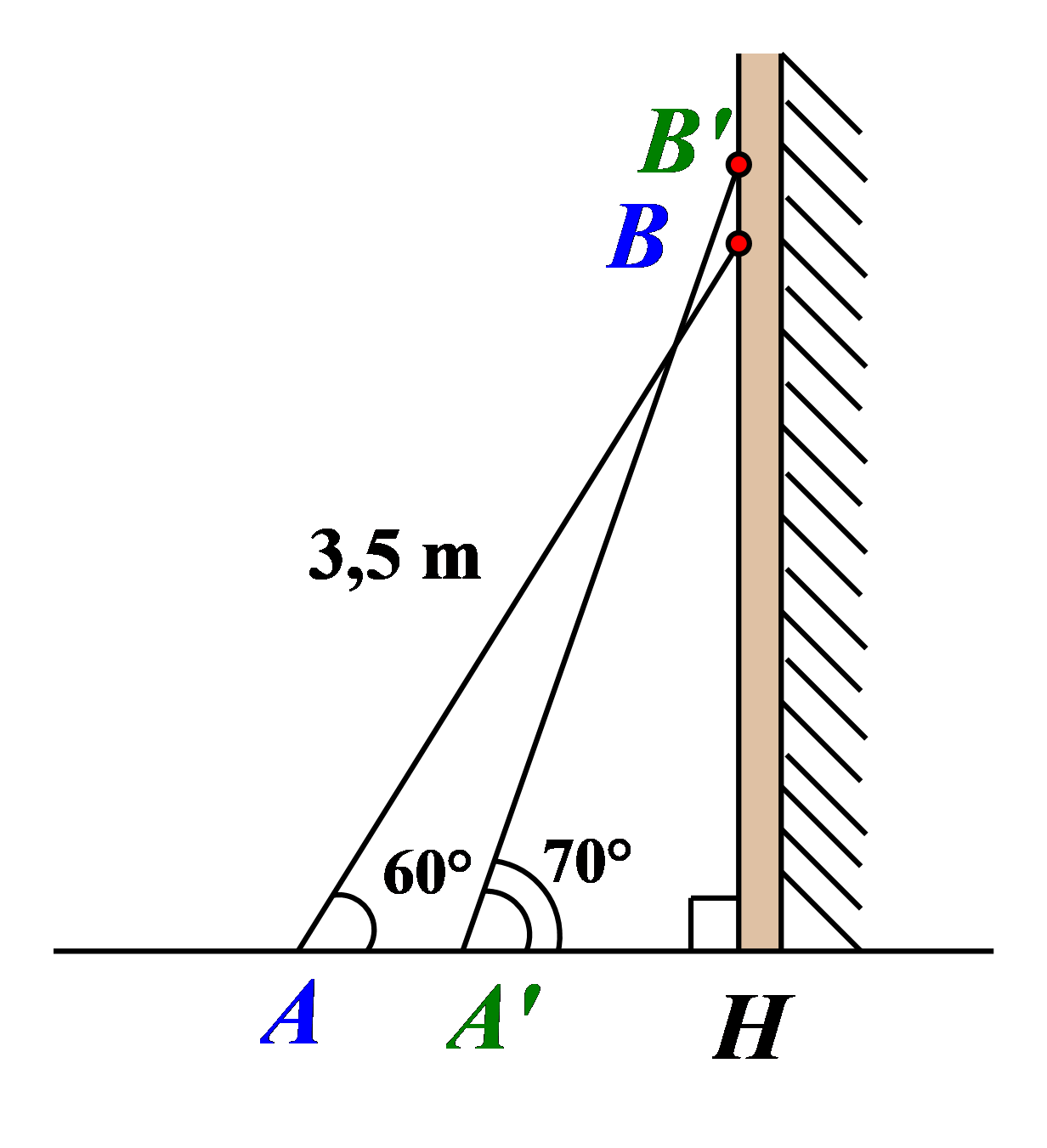
Gắn dữ kiện của bài toán vào mô hình Toán học như trên hình vẽ.
Khi thang tạo với mặt đất một góc có độ lớn \[6{\rm{0}}^\circ \] và \[7{\rm{0}}^\circ \] thì khoảng cách từ chân thang đến chân tường lần lượt là \[AH\] và \[A'H'\].
• Tam giác \[ABH\] vuông tại \[H\] có \[AH = AB \cdot \cos A = 3,5\cos 60^\circ = 1,75\,\,({\rm{m}})\].
• Tam giác \[A'B'H\] vuông tại \[H\] có \[A'H = A'B' \cdot \cos A' = 3,5\cos 70^\circ \approx 1,20\,\,({\rm{m}})\].
Do đó \[1,20\, \le x \le 1,75\].
Lời giải
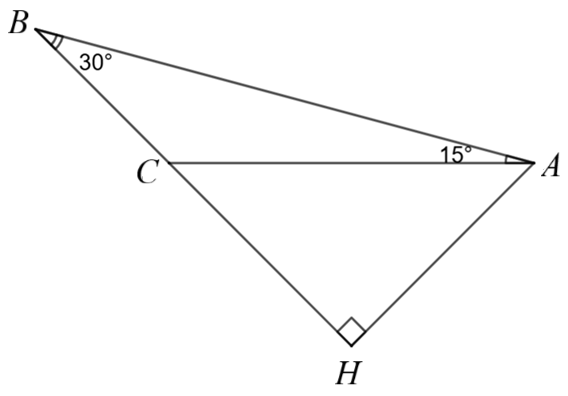
a) Sai. Xét \(\Delta ABC\) có \(\widehat A = 15^\circ \,;\,\,\widehat B = 30^\circ \) nên \(\widehat C = 180^\circ - 15^\circ - 30^\circ = 135^\circ \).
Tam giác \(ABC\) có \(\widehat C\) là góc tù nên tam giác \(ABC\) là tam giác tù.
b) Đúng. Xét \(\Delta HAB\) vuông tại \(H\) có: \(AH = AB \cdot \sin 30^\circ = 7,5\,\,({\rm{cm}}).\)
c) Đúng. Xét \(\Delta HAC\) vuông tại \(H\) có \(\widehat {ACH} = \widehat B + \widehat {CAB} = 45^\circ \) hay \(\Delta HAC\) vuông cân tại \(H.\)
d) Sai. Xét \(\Delta HAB\) vuông tại \(H\) có:\(BH = AB \cdot \cos 30^\circ = \frac{{15\sqrt 3 }}{2}\,\,({\rm{cm}}).\)
Vì \(\Delta HAC\)vuông cân tại \(H\) nên \(CH = 7,5\,\,{\rm{cm}}{\rm{.}}\)
Khi đó, \(BC = BH - CH \approx 5,49\,\,({\rm{cm}}).\)
Vậy \({S_{ABC}} = \frac{1}{2} \cdot AH \cdot BC = \frac{1}{2} \cdot 7,5 \cdot 5,49 = 20,59\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right) \approx 21\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\] Đáp án: 1906. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/62-1761201093.png)
![a) Độ dài \[AC\] đường dây (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/45-1761183430.png)
![Chọn D Ta có, góc tạo bởi cạnh \[AB\] và phương năm ngang trên mặt đất là \[\widehat {ABH}\]. Xét tam giác \[ABH\] vuôn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/8-1761181578.png)