Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nhỏ giữa biển đến vị trí con sao biển \[C\] trên bãi cát (như hình bên dưới), người ta chọn một điểm \[B\] trên bãi biển cách điểm \[C\] một khoảng \[1225\,\,{\rm{m}}\] và dùng giác kế ngắm xác định được \[\widehat {ABC} = {75^{\rm{o}}}\]; \[\widehat {ACB} = {65^{\rm{o}}}\]. Tính khoảng cách \[AC\] (kết quả làm tròn đến đơn vị mét).
![Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nh (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/43-1761183381.png)
a) \[\widehat {BAC} = 40^\circ {\rm{.}}\]
b) Tam giác \[ABC\] nhọn.
c) \[\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\].
d) Khoảng cách từ một gốc cây \[A\] trên một hòn đảo nhỏ giữa biển đến vị trí con sao biển \[C\] trên bãi cát là \[1625{\rm{ m}}{\rm{.}}\]
Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nhỏ giữa biển đến vị trí con sao biển \[C\] trên bãi cát (như hình bên dưới), người ta chọn một điểm \[B\] trên bãi biển cách điểm \[C\] một khoảng \[1225\,\,{\rm{m}}\] và dùng giác kế ngắm xác định được \[\widehat {ABC} = {75^{\rm{o}}}\]; \[\widehat {ACB} = {65^{\rm{o}}}\]. Tính khoảng cách \[AC\] (kết quả làm tròn đến đơn vị mét).
![Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nh (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/43-1761183381.png)
a) \[\widehat {BAC} = 40^\circ {\rm{.}}\]
b) Tam giác \[ABC\] nhọn.
c) \[\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\].
d) Khoảng cách từ một gốc cây \[A\] trên một hòn đảo nhỏ giữa biển đến vị trí con sao biển \[C\] trên bãi cát là \[1625{\rm{ m}}{\rm{.}}\]
Câu hỏi trong đề: Đề kiểm tra Toán 9 Kết nối tri thức Chương 4 có đáp án !!
Quảng cáo
Trả lời:
a) Đúng. Áp dụng định lý tổng ba góc trong một tam giác, ta có:
\[\widehat {BAC} = {180^{\rm{o}}} - \left( {\widehat {ABC} + \widehat {ACB}} \right) = 180^\circ - \left( {75^\circ + 65^\circ } \right) = 40^\circ .\]
b) Đúng. Vì \[\widehat {ABC} = 75^\circ \,;\,\,\widehat {ACB} = 65^\circ \] và \[\widehat {BAC} = 40^\circ \] nên \[\Delta ABC\] nhọn.
c) Đúng. Xét tam giác nhọn \[ABC\], kẻ các đường cao \[BD,\,\,CE\] thì các đường cao này nằm trong tam giác (như hình vẽ) có \[a = BC;\,\,b = AC;\,\,c = AB\].
![Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nh (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/10/44-1761183405.png)
Xét \[\Delta ADB\] vuông tại \[D\], áp dụng hệ thức giữa cạnh và góc nhọn trong tam giác vuông ta có:
\[BD = AB \cdot \sin \widehat {BAC} = c \cdot \sin A.\] \[\left( 1 \right)\]
Xét \[\Delta CDB\] vuông tại \[D\], áp dụng hệ thức giữa cạnh và góc nhọn trong tam giác vuông ta có:
\[BD = BC \cdot \sin \widehat {ACB} = a \cdot \sin C.\] \[\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[c \cdot \sin A = a \cdot \,\sin C\] hay \[\frac{a}{{\sin A}} = \frac{c}{{\sin C}}.\]
Chứng minh tương tự, ta được \[b \cdot \sin A = a \cdot \sin B\] hay \[\frac{a}{{\sin A}} = \frac{b}{{\sin B}}.\]
Do đó \[\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\] hay \[\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\].
d) Sai. Từ câu c, ta có: \[\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\].
Suy ra \[\frac{{1225}}{{\sin 40^\circ }} = \frac{{AC}}{{\sin 75^\circ }}\] hay \[AC = \frac{{1\,\,225 \cdot \sin 75^\circ }}{{\sin 40^\circ }} \approx 1841\,\,{\rm{(m)}}{\rm{.}}\]
Vậy khoảng cách \[AC\] là \[1841{\rm{ m}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
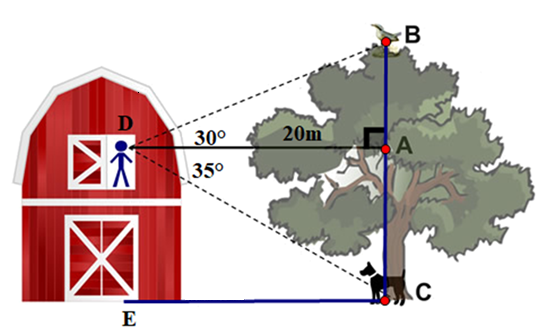
Tứ giác \[ADEC\] là hình chữ nhật nên \(DA = EC = 20\;\,{\rm{m}}\).
• Xét \(\Delta ACD\) vuông tại \[A,\] ta có:
\[\tan \widehat {ADC} = \frac{{AC}}{{AD}}\] hay \[\tan 35^\circ = \frac{{AC}}{{20}}\] nên \[AC = 20 \cdot \tan 35^\circ \approx 14\;\,({\rm{m}})\].
• Xét \(\Delta ABD\) vuông tại A, ta có:
\[\tan \widehat {ADB} = \frac{{AB}}{{AD}}\] hay \[\tan 30^\circ = \frac{{AB}}{{20}}\] nên \[AB = 20 \cdot \tan 30^\circ \approx 12\;\,({\rm{m}})\].
Do đó \(BC = BA + AC = 14 + 12 = 26\;\,\,({\rm{m)}}{\rm{.}}\)
Vậy chiều cao \[AB\] của cây xoài là \[26{\rm{ m}}.\]
Đáp án: 26.
Lời giải
Lời giải
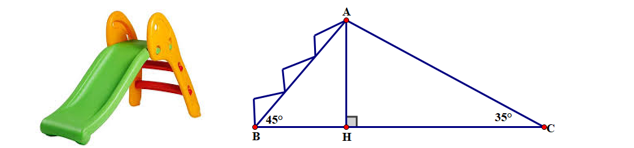
Xét \(\Delta ABH\) vuông tại \(A\), ta có:
\(\tan B = \frac{{AH}}{{AB}}\) hay \(\tan 63^\circ = \frac{{AH}}{{235}}\) nên \(AH = 235 \cdot \tan 63^\circ = 461\;\,({\rm{m)}}\).
Vậy chiều cao của tòa nhà này là \[461{\rm{ m}}.\]
Đáp án: 461.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Lời giải Xét \(\Delta ABH\) vuông tại \(A\), ta có: \(\tan B = \frac{{AH}}{{AB}}\) hay \(\tan 63^\circ = \frac{{AH}}{{235}}\) nên \(AH = 235 \cdot \tan 63^\circ = 461\;\,({\rm{m)}}\). Vậy chiều cao của tòa nhà này là \[461{\rm{ m}}.\] Đáp án: 461. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/67-1761202758.png)
![Chọn D Tam giác \[AHB\] v (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/21-1761182141.png)
![\[x \approx 4,9{\rm{\;(m)}} \approx {\rm{5\;m}}{\rm{.}}\] Do đó điểm gãy cách gốc k (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/6-1761204118.png)