Đề kiểm tra Toán 9 Kết nối tri thức Chương 4 có đáp án - Đề 2
20 người thi tuần này 4.6 831 lượt thi 11 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Trắc nghiệm Tổng hợp Toán năm 2024 có đáp án - Phần 19
Trắc nghiệm Tổng hợp Toán năm 2024 có đáp án - Phần 18
Trắc nghiệm Tổng hợp Toán năm 2024 có đáp án - Phần 17
Bài tập Tình diện tích mặt ngoài, thể tích của hình hỗn hợp có liên quan hình cầu lớp 9 (có lời giải)
Trắc nghiệm Tổng hợp Toán năm 2024 có đáp án - Phần 16
Trắc nghiệm Tổng hợp Toán năm 2024 có đáp án - Phần 15
Trắc nghiệm Tổng hợp Toán năm 2024 có đáp án - Phần 14
Bài tập Giải bài toán bằng cách lập phương trình lớp 9 (có lời giải)
Danh sách câu hỏi:
Câu 1/11
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
Chọn C
Vì \[\alpha ,\,\,\beta \] là hai góc phụ nhau nên \[\beta = 90^\circ - \alpha .\]
Theo định lí tỉ số lượng giác của hai góc phụ nhau, ta có:
\[\sin \alpha = \cos \left( {90^\circ - \alpha } \right) = \cos \beta ;\] \[\tan \alpha = \cot \left( {90^\circ - \alpha } \right) = \cot \beta .\]
Câu 2/11
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn A
Trong một tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối.
Câu 3/11
![Chọn D Tam giác \[AHB\] v (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/21-1761182141.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn D
Tam giác \[AHB\] vuông tại \[H\] có \[\tan A = \tan \alpha = \frac{{BH}}{{AH}} = \frac{{2,4}}{{25}} = \frac{{11}}{{125}}\] nên \[\alpha \approx {\rm{5}}^\circ 29'.\]
Vậy góc tạo bởi đường đi của quả bóng và mặt đất là \[\alpha \approx {\rm{5}}^\circ 29'.\]
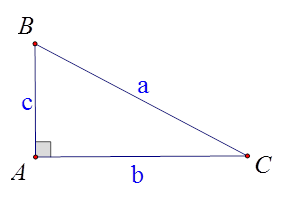
Câu 4/11
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn B
![Vì tam giác \[ABC\] vuông tại \[C\ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/4-1761204036.png)
Áp dụng định lí Pythagore cho tam giác \[ABC\] vuông tại \[C\], ta được:
\[B{C^2} = A{B^2} - A{C^2} = 1,{5^2} - 1,{2^2} = 0,81.\]
Suy ra \[BC = 0,9{\rm{\;(cm)}}{\rm{.}}\]
Vì tam giác \[ABC\] vuông tại \[C\] nên \[\tan B = \frac{{AC}}{{BC}} = \frac{{1,2}}{{0,9}} = \frac{4}{3}.\]
Câu 5/11
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn B
![Chọn B Vì tam giác \[ABC\] vuông tại \[A\] nên \[AC = BC.\sin B = 12.\sin 40^\circ \approx 7,71\] (cm). Tam giác \[A (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/5-1761204085.png)
Vì tam giác \[ABC\] vuông tại \[A\] nên \[AC = BC.\sin B = 12.\sin 40^\circ \approx 7,71\] (cm).
Tam giác \[ABC\] vuông tại \[A\] nên \[\widehat B + \widehat C = 90^\circ \] (tổng hai góc nhọn của tam giác vuông).
Suy ra \[\widehat C = 90^\circ - \widehat B = 90^\circ - 40^\circ = 50^\circ .\]
Câu 6/11
![\[x \approx 4,9{\rm{\;(m)}} \approx {\rm{5\;m}}{\rm{.}}\] Do đó điểm gãy cách gốc k (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/6-1761204118.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn B
Ta mô hình hóa bài toán như hình vẽ trên.
Khoảng cách từ gốc cây đến điểm bị gãy là \[AB.\]
Khoảng cách từ điểm thân tre bị gãy đến ngọn cây là \[BC.\]
Khoảng cách từ ngọn cây chạm đất đến gốc là \[AC.\]
Đặt độ dài \(BC = x{\rm{\;(m)}}\,\,\left( {0 < x < 9} \right)\).
Suy ra: \(AB = 9 - x.\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(AB = BC \cdot \cos B\)
Suy ra \(9 - x = x \cdot \cos 32^\circ \)
\(9 - x \approx 0,85x\)
\(1,85x \approx 9\)
\[x \approx 4,9{\rm{\;(m)}} \approx {\rm{5\;m}}{\rm{.}}\]
Do đó điểm gãy cách gốc khoảng \(5\) m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nh (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/43-1761183381.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Lời giải Xét \(\Delta ABH\) vuông tại \(A\), ta có: \(\tan B = \frac{{AH}}{{AB}}\) hay \(\tan 63^\circ = \frac{{AH}}{{235}}\) nên \(AH = 235 \cdot \tan 63^\circ = 461\;\,({\rm{m)}}\). Vậy chiều cao của tòa nhà này là \[461{\rm{ m}}.\] Đáp án: 461. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/67-1761202758.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 5/11 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập