PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
An và Bình chơi bài. Người thua phải trả 1 cây kẹo cho người thắng trong ván đầu tiên; 2 cây kẹo trong ván thứ 2; 4 cây kẹo trong ván thứ 3 và cứ thế số kẹo mỗi lần thua tăng gấp đôi so với lần trước đó. Ban đầu An có 625 cây kẹo và sau 10 ván thì An thua hết kẹo (có ván thắng, có ván thua). An nói với Bình: “Nếu chúng ta không chơi theo luật vừa rồi mà chơi theo luật khác: ván đầu người thua trả 10 cây cho người thắng, ván 2 trả 20 cây, ván 3 trả 30 cây thì tớ vẫn còn chơi với cậu được vài ván nữa”. Vậy, bạn An nói đúng hay sai?
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
An và Bình chơi bài. Người thua phải trả 1 cây kẹo cho người thắng trong ván đầu tiên; 2 cây kẹo trong ván thứ 2; 4 cây kẹo trong ván thứ 3 và cứ thế số kẹo mỗi lần thua tăng gấp đôi so với lần trước đó. Ban đầu An có 625 cây kẹo và sau 10 ván thì An thua hết kẹo (có ván thắng, có ván thua). An nói với Bình: “Nếu chúng ta không chơi theo luật vừa rồi mà chơi theo luật khác: ván đầu người thua trả 10 cây cho người thắng, ván 2 trả 20 cây, ván 3 trả 30 cây thì tớ vẫn còn chơi với cậu được vài ván nữa”. Vậy, bạn An nói đúng hay sai?Câu hỏi trong đề: Bộ 19 đề thi Giữa kì 1 Toán 11 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Theo cách nói của An và xem như An thua tất cả các ván bài. Khi đó, số kẹo thua mỗi ván lập thành cấp số cộng với số hạng đầu \[{u_1} = 10\] và công sai \[d = 10\].
Giả sử sau \[n\] ván thì An thua hết kẹo.
Khi đó: \[{S_n} = {u_1} + {u_2} + ... + {u_n} = 625\]
\[ \Leftrightarrow n.{u_1} + \frac{{n\left( {n - 1} \right)}}{2}d = 625 \Leftrightarrow 10n + \frac{{n\left( {n - 1} \right)}}{2}.10 = 625 \Leftrightarrow 5{n^2} + 5n - 625 = 0 \Leftrightarrow \left[ \begin{array}{l}n \approx 10,7\\n \approx - 11,7\end{array} \right.\] \[ \Leftrightarrow n \approx 10,7\]
Vậy, An nói đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn hệ trục tọa độ trong mặt phẳng tọa độ \(Oxy\)như sau
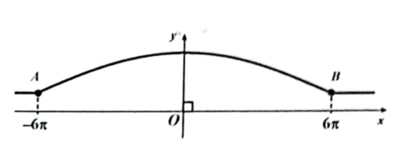
Trong đó trục \[Ox\]mô tà là mặt nước thủy triều của sông; trục Oy là khoảng cách giửa đỉnh cầu và mặt nước thủy triều của sông.
Xét điểm \[M\left( {x;y} \right)\]nằm trên cung\[AB\], khoảng cách từ điểm \[M\left( {x;y} \right)\]đến mặt nước tương ứng với giá trị tung độ \[y\]của điểm \[M\].
Xét phương trình \(\frac{8}{{\sqrt 3 }}\cos \frac{x}{{12}} + 2 = 5,2 + 0,8 \Leftrightarrow \cos \frac{x}{{12}} = \frac{{\sqrt 3 }}{2}\)
Vì \(x \in \left[ { - 6\pi ;6\pi } \right] \Rightarrow \frac{x}{{12}} \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\)
Nên \(\cos \frac{x}{{12}} = \frac{{\sqrt 3 }}{2} \Leftrightarrow \frac{x}{{12}} = \pm \frac{\pi }{6} \Leftrightarrow x = \pm 2\pi hay\left| x \right| = 2\pi \)
Để sà lan có thể đi qua được gầm cầu đúng qui định thì bề rộng khối hàng là
\(2\left| x \right| = 4\pi = 4x3,14 = 12,56 \approx 12,6\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
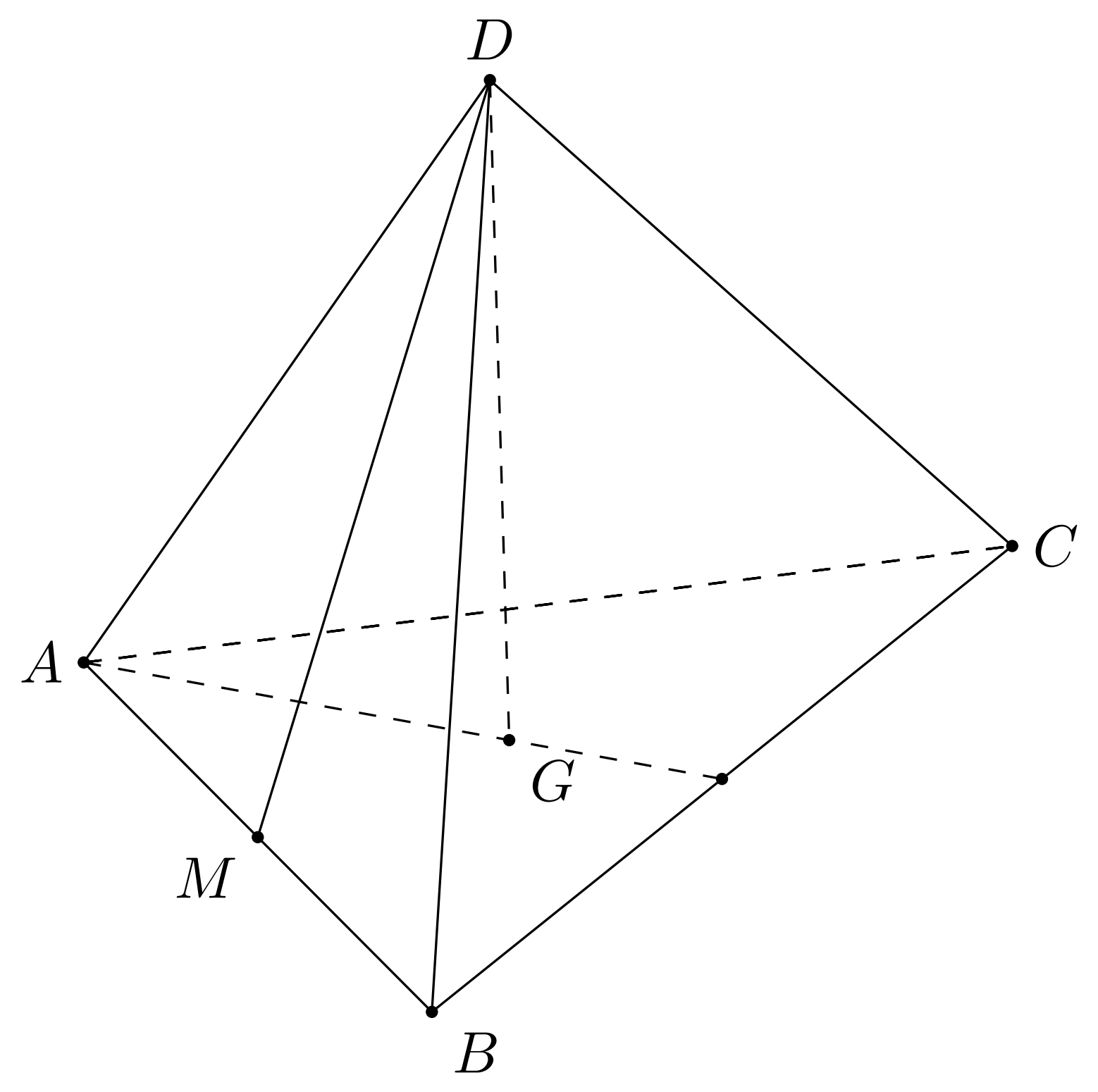
Gọi \(M\) là trung điểm \(AB\).
Khi đó cắt tứ diện bởi mặt phẳng \((GCD)\) ta được thiết diện là \(\Delta MCD\).
Ta có tứ diện đều \(ABCD\) có cạnh bằng \(2 \Rightarrow MC = MD = \frac{{2\sqrt 3 }}{2} = \sqrt 3 \); \(CD = 2\).
Khi đó nửa chu vi \(\Delta MCD\): \(p = \frac{{\sqrt 3 + \sqrt 3 + 2}}{2} = 1 + \sqrt 3 \).
Nên \({S_{\Delta MCD}} = \sqrt {p(p - MC)(p - MD)(p - CD)} = \sqrt 2 = 1,4\)
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập