PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.

Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kỹ sư theo phương thức sau: Mức lương của quý làm việc đầu tiên cho công ty là \(13,5\) triệu đồng/quý, và kể từ quý làm việc thứ hai, mức lương sẽ được tăng thêm \(500.000\) đồng mỗi quý. Tính tổng số tiền lương một kỹ sư nhận được sau ba năm làm việc cho công ty.

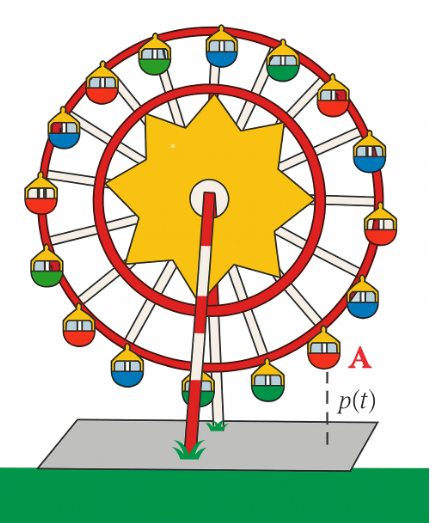
Ta có: \(20 + 10\sin \left( {\frac{{\pi \left( {t - 1} \right)}}{5}} \right) = 30 \Leftrightarrow \sin \left( {\frac{{\pi \left( {t - 1} \right)}}{5}} \right) = 1\) Ÿ

\( \Leftrightarrow \frac{{\pi \left( {t - 1} \right)}}{5} = \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)\( \Leftrightarrow t = 1 + \frac{5}{2} + 10k = \frac{7}{2} + 10k\left( {k \in \mathbb{Z}} \right)\)Ÿ

Vì \(0 \le t \le 10\)\( \Rightarrow 0 \le \frac{7}{2} + 10k \le 10 \Leftrightarrow  - 0,35 \le k \le 0,65\) Ÿ

Mà \(k \in \mathbb{Z}\) nên \(k = 0\). Suy ra \(t = 3,5\)(giây).Ÿ

Vậy trong 10 giây đầu tiên, tại thời điểm ra \(t = 3,5\)(giây) thì độ cao của buồng A đạt 30 mét.

(Sai) Có đúng \(2\) mặt phẳng phân biệt chứa điểm \(O\) trong các mặt phẳng được tạo từ \(5\) điểm \(S,A,B,C,D\)
(Vì): Vì các mặt phẳng thỏa mãn yêu cầu chứa điểm \(O\) gồm \((SAC);(SBD);(ABCD)\).
(Đúng) Giao tuyến của hai mặt phẳng \((MBD)\) và \((SAC)\) là đường thẳng \(OM\)
(Vì): Vì ta có \(\left\{ {\begin{array}{*{20}{l}}{M \in (MBD)({\rm{v\`i}}M \in SA)}\end{array}} \right. \Rightarrow M \in (MBD) \cap (SAC)(1)\).
Tương tự \(\left\{ {\begin{array}{*{20}{l}}{O \in (MBD)({\rm{v\`i}}O \in BD)({\rm{v\`i}}O \in AC)}\end{array}} \right. \Rightarrow O \in (MBD) \cap (SAC)(2)\).
Từ \((1)\) và \((2)\) suy ra \(OM = (SAC) \cap (MBD)\).
(Sai) Giao tuyến của hai mặt phẳng \((DMN)\) và \((SAC)\) là đường thẳng \(ME\) với \(E\) là trung điểm của đoạn thẳng \(OC\)
(Vì): Vì ta có \(\left\{ {\begin{array}{*{20}{l}}{M \in (DMN)}\\{M \in (SAC)({\rm{v\`i}}M \in SA)}\end{array}} \right. \Rightarrow M \in (DMN) \cap (SAC)(3)\).
Trong mặt phẳng \((ABCD)\) gọi \(E = DN \cap AC\).
Ta có \(\left\{ {\begin{array}{*{20}{l}}{E \in (DMN)({\rm{v\`i}}E \in DN)}\\{E \in (SAC)({\rm{v\`i}}E \in AC)}\end{array}} \right. \Rightarrow E \in (DMN) \cap (SAC)(4)\).
Từ \((3)\) và \((4)\) suy ra \(ME = (DMN) \cap (SAC)\).
Tam giác \(BCD\) có \(E = DN \cap OC\) và \(DN,OC\) là hai đường trung tuyến.
Suy ra \(E\) là trọng tâm của tam giác \(BCD\).
(Đúng) Giao điểm giữa đường thẳng \(CM\) và mặt phẳng \((SBD)\) là trọng tâm tam giác \(SAC\)
(Vì): Vì trong mặt phẳng \((SAC)\) gọi \(F = CM \cap SO\).
Ta có \(\left\{ {\begin{array}{*{20}{l}}{F \in CM}\\{F \in (SAC)({\rm{v\`i}}F \in SO \subset (SAC))}\end{array}} \right. \Rightarrow F = CM \cap (SAC)\).
Tam giác \(SAC\) có \(F = CM \cap SO\) và \(SO,CM\) là hai đường trung tuyến.
Suy ra \(F\) là trọng tâm của tam giác \(SAC\).