Cho hình chóp \(S.ABCD\)có đáy \(ABCD\)là hình thang, \(AD{\rm{//}}BC\), \(AD = 2BC\). \(M\)là trung điểm của \(SA\). Mặt phẳng \(\left( {MBC} \right)\)cắt hình chóp theo thiết diện là
A. Hình bình hành.
B. Tam giá
C. Hình chữ nhật.
D. Hình thang.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A
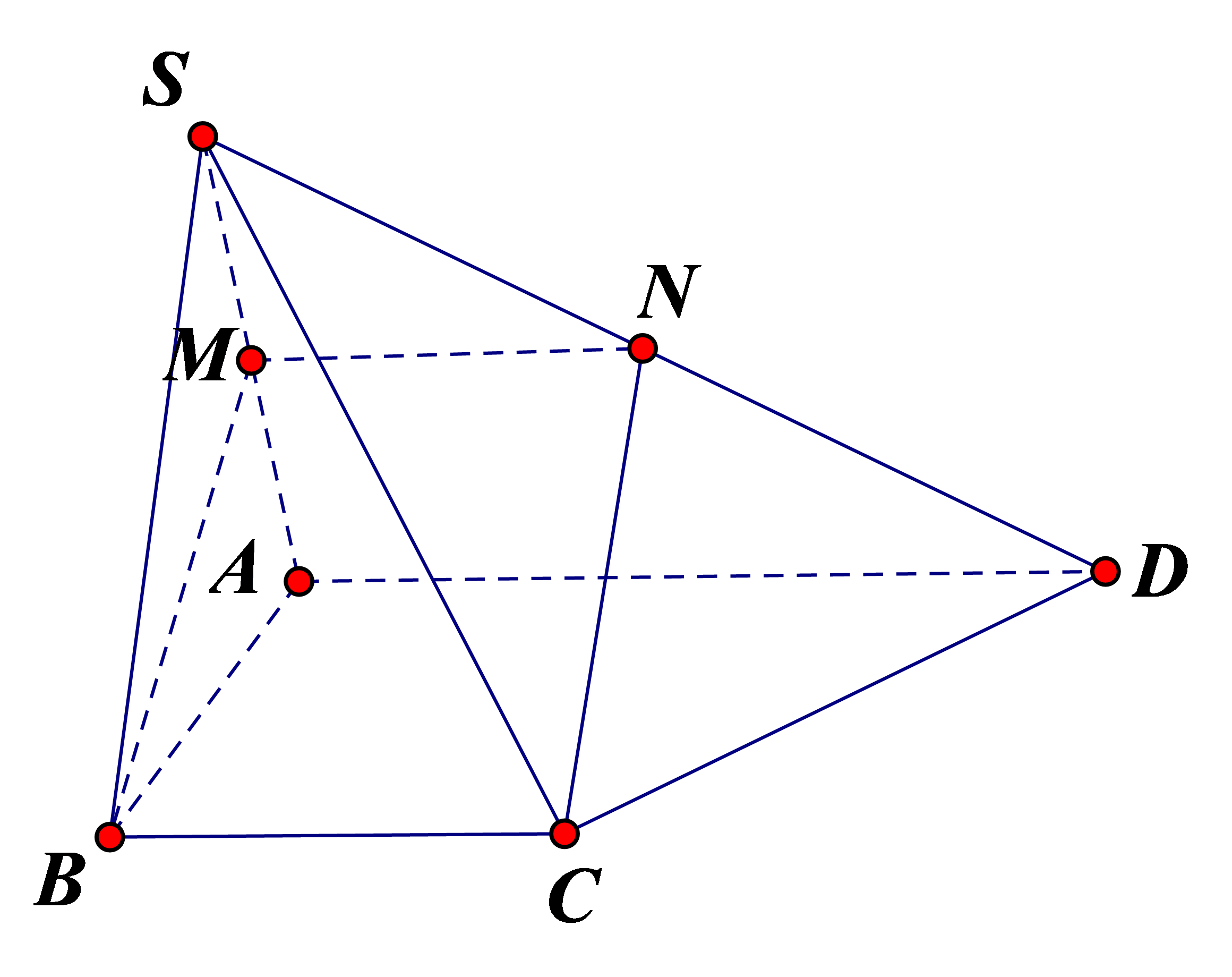
Ta có \(\left( {BMC} \right) \cap \left( {ABCD} \right) = BC\), \(\left( {BMC} \right) \cap \left( {SAB} \right) = BM\)\(\left( {BMC} \right) \cap \left( {SAD} \right) = {M_x},\,{M_x}{\rm{//}}AD{\rm{//}}BC,\,{M_x} \cap SD = N\), \(\left( {BMC} \right) \cap \left( {SCD} \right) = NC\)
Suy ra thiết diện của hình chóp cắt bởi mặt phẳng \(\left( {MBC} \right)\)là tứ giác \(BMNC\).
Ta có \(\left\{ \begin{array}{l}MN = \frac{1}{2}AD\\MN{\rm{//}}AD\end{array} \right.\)suy ra \(\left\{ \begin{array}{l}MN = BC\\MN{\rm{//BC}}\end{array} \right.\)nên thiết diện \(BMNC\)là hình bình hành.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
![Cho hình chóp \[S.ABCD\], đáy \[ABCD\] là hình thang, đáy lớn \[AB\]. Gọi \[N,P\] lần lượt là trung điểm của \[SA,SB\]. \[M\] là một điểm tùy ý thuộc đoạn \[SD\] (\[M\] không trùng với \[D\]). Tìm giao điểm của \[SC\] với \[(MNP)\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/2-1761549756.jpg)
Chọn \({\rm{mp}}\left( {SBC} \right)\) chứa \[SC\]
Ta có \(FP = \left( {MNP} \right) \cap \left( {SBC} \right)\)
Gọi \(G = FP \cap SC\)
Suy ra \(G = SC \cap \left( {MNP} \right)\)
Lời giải
Theo giả thiết ta có công thức tăng trưởng dân số \({P_n} = {P_0}.{\left( {1 + r} \right)^n}\).
Trong đó \({P_0} = 97,58\,\) và \(r = 1,14\% \);\(n = 2025 - 2020 = 5\).
Vậy từ năm 2020 đến thì 2025 dân số nước ta là \(97,58.1,{0114^5} \approx 103\) (triệu người).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Một tam giác hoặc một ngũ giác.
B. Một tứ giác hoặc một ngũ giác.
C. Một tam giác và một hình bình hành.
D. Một tam giác hoặc một tứ giác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. giếng \(20\)\[\left( {\rm{m}} \right)\]chọn A còn giếng \(25\)\[\left( {\rm{m}} \right)\]chọn B
B. luôn chọn B
C. giếng \(20\)\[\left( {\rm{m}} \right)\]chọn B còn giếng \(25\)\[\left( {\rm{m}} \right)\]chọn B
D. luôn chọn A
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo