PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{ - {x^2} + 2(m + 1)x - 5}}{{x - 1}}\).
a) Để hàm số có cực đại, cực tiểu thì \(m > 4\).
b) Khi \(m = 0\) thì đồ thị hàm số không cắt \(Ox\).
c) Khi \(m = 0\) thì đồ thị hàm số có tiệm cận xiên là \(y = - x + 1\).
d) Tồn tại 1 điểm \(M\) thuộc đồ thị \((C)\) sao cho \({x_M} > 1\) và độ dài \(IM\) ngắn nhất (\[I\] là tâm đối xứng của \((C)\)) khi đó tung độ \({y_M} < - 4\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{ - {x^2} + 2(m + 1)x - 5}}{{x - 1}}\).
a) Để hàm số có cực đại, cực tiểu thì \(m > 4\).
b) Khi \(m = 0\) thì đồ thị hàm số không cắt \(Ox\).
c) Khi \(m = 0\) thì đồ thị hàm số có tiệm cận xiên là \(y = - x + 1\).
d) Tồn tại 1 điểm \(M\) thuộc đồ thị \((C)\) sao cho \({x_M} > 1\) và độ dài \(IM\) ngắn nhất (\[I\] là tâm đối xứng của \((C)\)) khi đó tung độ \({y_M} < - 4\).
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
(a)(b) Khi \(m = 0:y = \frac{{ - {x^2} + 2x - 5}}{{x - 1}} = - x + 1 - \frac{4}{{x - 1}}\)
Tâp xác định \(D = \mathbb{R}\backslash \{ 1\} \)
\(\begin{array}{l}{y^\prime } = \frac{{ - {x^2} + 2x + 3}}{{{{(x - 1)}^2}}}\\{y^\prime } = 0 \Leftrightarrow - {x^2} + 2x + 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1 \Rightarrow y = 4}\\{x = 3 \Rightarrow y = - 4}\end{array}} \right.\\\mathop {\lim }\limits_{x \to 1 \mp } y = \pm \infty :x = 1{\rm{ l\`a tcd }}\\\mathop {\lim }\limits_{x \to \pm \infty } y = - x + 1:y = - x + 1{\rm{ l\`a tcx}}\end{array}\)
Bảng biến thiên:
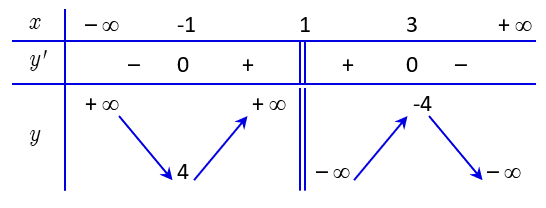
\(\begin{array}{l}x = 0 \Rightarrow y = 5\\y = 0 \Rightarrow - {x^2} + 2x - 5 = 0{\rm{ (v\^o nghiem) }}\end{array}\)
Đồ thị hàm số không cắt \(Ox\).
(c) \(y = \frac{{ - {x^2} + 2(m + 1)x - m - 5}}{{x - 1}}\)
\({y^\prime } = \frac{{ - {x^2} + 2x - 2m - 2 + m + 5}}{{{{(x - 1)}^2}}} = \frac{{ - {x^2} + 2x - m + 3}}{{{{(x - 1)}^2}}}\)
Hàm số \[y\] có cực đại cực tiểu khi phương trình \( - {x^2} + 2x - m + 3 = 0\) có hai nghiệm phân biệt \( \Leftrightarrow {\Delta ^\prime } = 1 - m + 3 = 4 - m > 0 \Leftrightarrow m < 4,x = 1\) không phải là nghiệm của phương trình \({y^\prime } = 0 \Leftrightarrow - 1 + 2 - m + 3 \ne 0\) \( \Leftrightarrow m \ne 4\)
Điều kiện sau cùng: \(m < 4\)
(d) \({x_M} > 1 \Rightarrow M\) thuộc nhánh bên phải của \((C).I(1,0)\)
\(\begin{array}{*{20}{l}}{}&{\left. {M(m, - m + 1 - \frac{4}{{m - 1}}} \right)}\\{}&{I{M^2} = {{(m - 1)}^2} + \left[ {{{( - m + 1)}^2} + \frac{{16}}{{{{(m - 1)}^2}}} + 8} \right]}\\{}&{ = 2{{(m - 1)}^2} + \frac{{16}}{{{{(m - 1)}^2}}} + 8 \ge 2\sqrt 2 (m - 1) \cdot \frac{4}{{(m - 1)}} + 8}\\{ \Rightarrow I{M^2}}&{ \ge 8(\sqrt 2 + 1) \Rightarrow IM \ge \sqrt {8(\sqrt 2 + 1)} }\end{array}\)
\[IM\]ngắn nhất khi \(2{(m - 1)^2} = \frac{{16}}{{{{(m - 1)}^2}}} \Leftrightarrow {(m - 1)^4} = 8 \Leftrightarrow m = 1 + \sqrt[4]{8}\)
\( \Rightarrow {y_M} = - \sqrt[4]{8} - \frac{4}{{\sqrt[4]{8}}} < - 4\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
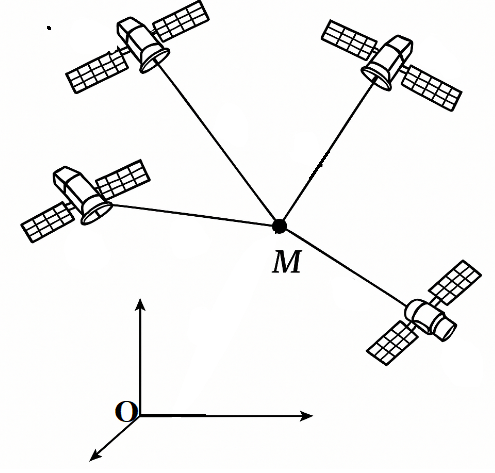
Do vị trí \(M(a;b;c)\) thỏa mãn \(MA = 3,\,MB = 6,\,MC = 5,\,MD = 13\)
\[\overrightarrow {AM} = \left( {a - 3;b - 1;c} \right) \Rightarrow {\left( {a - 3} \right)^2} + {\left( {b - 1} \right)^2} + {c^2} = {3^2}\]
\[ \Rightarrow {a^2} + {b^2} + {c^2} - 6a - 2b + 1 = 0\left( 1 \right)\]
\[\overrightarrow {BM} = \left( {a - 3;b - 6;c - 6} \right) \Rightarrow {\left( {a - 3} \right)^2} + {\left( {b - 6} \right)^2} + {\left( {c - 6} \right)^2} = {6^2}\]
\[ \Rightarrow {a^2} + {b^2} + {c^2} - 6a - 12b - 12c + 45 = 0\left( 2 \right)\]
\[\overrightarrow {CM} = \left( {a - 4;b - 6;c - 2} \right) \Rightarrow {\left( {a - 4} \right)^2} + {\left( {b - 6} \right)^2} + {\left( {c - 2} \right)^2} = {5^2}\]
\[ \Rightarrow {a^2} + {b^2} + {c^2} - 8a - 12b - 4c + 31 = 0\left( 3 \right)\]
\[\overrightarrow {DM} = \left( {a - 6;b - 2;c - 14} \right) \Rightarrow {\left( {a - 6} \right)^2} + {\left( {b - 2} \right)^2} + {\left( {c - 14} \right)^2} = {13^2}\]
\[ \Rightarrow {a^2} + {b^2} + {c^2} - 12a - 4b - 28c + 67 = 0\left( 4 \right)\]
Từ \(\left( 1 \right),\,\left( 2 \right),\,\left( 3 \right),\,\left( 4 \right)\) ta có hệ phương trình \[ \Leftrightarrow \left\{ \begin{array}{l}10b + 12c = 44\\2a + 10b + 4c = 30\\6a + 2b + 28c = 66\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = 2\end{array} \right.\]
\[ \Rightarrow M\left( {1;2;2} \right) \Rightarrow \overrightarrow {OM} \left( {1;2;2} \right) \Rightarrow OM = \sqrt {{1^2} + {2^2} + {2^2}} = 3\].
Vậy khoảng cách từ điểm \(M\) đến điểm \(O\) bằng \(3\).
Lời giải
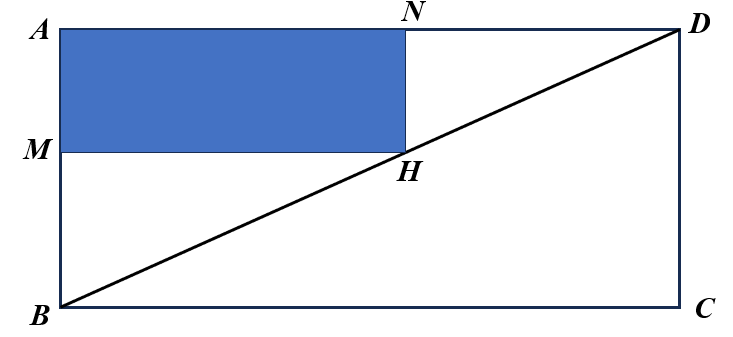
Vì \(\Delta DHN\) đồng dạng với \(\Delta DBA\) nên \(\frac{{DN}}{{DA}} = \frac{{NH}}{{AB}} = x\), với \(0 < x < 1\).
Khi đó \(NH = x.AB\); \(DN = x.DA \Rightarrow AN = \left( {1 - x} \right)DA\).
Ta có \({S_{AMHN}} = AN.NH = x\left( {1 - x} \right).AB.DA = x\left( {1 - x} \right){S_{ABCD}} = 25x\left( {1 - x} \right)\).
Số tiền người chủ cần chuẩn bị để trồng cỏ là \(80.25x\left( {1 - x} \right)\) (nghìn đồng).
Để số tiền lớn nhất thì \(f\left( x \right) = x\left( {1 - x} \right)\) đạt giá trị lớn nhất trên khoảng \(\left( {0;1} \right)\).
Nhận thấy \(f\left( x \right) = x\left( {1 - x} \right) = x - {x^2} = \frac{1}{4} - {\left( {\frac{1}{2} - x} \right)^2} \le \frac{1}{4},\forall x \in \left( {0;1} \right)\). Dấu bằng xảy ra khi và chỉ khi \(x = \frac{1}{2}\).
Vậy số tiền lớn nhất người chủ cần chuẩn bị để trồng cỏ là \(500\) (nghìn đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Ngày khai giảng năm học \(2024 - 2025\). Học sinh khối \(12\) trường THPT Nguyễn Hiền thả chùm bóng bay gắn thông điệp “Học Sinh khối \(12\) chiến thắng CT\(2018\)”. Ước tính độ cao \(h\)(tính bằng\(km\)) của chùm bóng bay so với mặt đất vào thời điểm\(t\) (đơn vị giờ) được cho bởi công thức \(h\left( t \right) = - {t^3} + 3{t^2},\left( {0 \le t \le 3} \right)\). Chùm bóng bay đạt độ cao lớn nhất so với mặt đất là: \(a\left( {km} \right)\). Tìm \(a?\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Ngày khai giảng năm học \(2024 - 2025\). Học sinh khối \(12\) trường THPT Nguyễn Hiền thả chùm bóng bay gắn thông điệp “Học Sinh khối \(12\) chiến thắng CT\(2018\)”. Ước tính độ cao \(h\)(tính bằng\(km\)) của chùm bóng bay so với mặt đất vào thời điểm\(t\) (đơn vị giờ) được cho bởi công thức \(h\left( t \right) = - {t^3} + 3{t^2},\left( {0 \le t \le 3} \right)\). Chùm bóng bay đạt độ cao lớn nhất so với mặt đất là: \(a\left( {km} \right)\). Tìm \(a?\)Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.