PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\) có đồ thị là đường cong \((C)\).

              a) Biết hàm số có 2 điểm cực trị khi đó tổng của giá trị cực đại và giá trị cực tiểu bằng \( - 4\).

              b) Để phương trình \({x^2} + 3x + 3 = m|x + 2|\) có 4 nghiệm phân biệt thì \(m > 2\).

              c) Đường tiệm cận xiên của đồ thị hàm số đi qua điểm \(A\left( {0;1} \right)\).

d) Phương trình tiếp tuyến với \((C)\) vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2},\frac{3}{2}} \right)\).

a)b) \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}} = x + 1 + \frac{1}{{x + 2}}\)

Tâp xác định: \(D = \mathbb{R}\backslash \{  - 2\} \)

\(\begin{array}{l}{y^\prime } = \frac{{{x^2} + 4x + 3}}{{{{(x + 2)}^2}}},{y^\prime } = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x =  - 1 \Rightarrow y = 1}\\{x =  - 3 \Rightarrow y =  - 3}\end{array}} \right.\\\mathop {\lim }\limits_{x \to  - 2 \pm } y =  \pm \infty :x =  - 2{\rm{ l\`a  tcd }}\\\mathop {\lim }\limits_{x \to  \pm x} y = x + 1 \Rightarrow y = x + 1{\rm{ l\`a  tcx}}\end{array}\)

Bảng biến thiên:

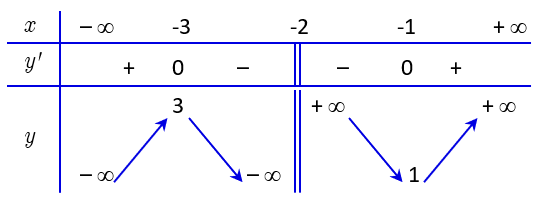
\(x = 0 \Rightarrow y = \frac{3}{2}\)

Đồ thị không cắt trục \(Ox\)

Đồ thị:

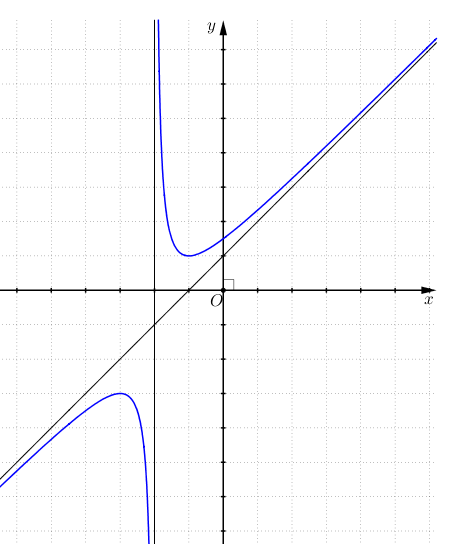
Đường thẳng \(x - 3y - 6 = 0\) có hệ số góc \({k_1} = \frac{1}{3} \Rightarrow \) tiếp tuyến của

(C) vuông góc với đường thẳng này có hệ số góc \({k_2} =  - 3\)

Xét phương trình \(y_x^\prime  =  - 3\)

\(\begin{array}{l} \Leftrightarrow \frac{{{x^2} + 4x + 3}}{{{{(x + 2)}^2}}} =  - 3 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne  - 2}\\{{x^2} + 4x + 3 =  - 3{x^2} - 12x - 12}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne  - 2}\\{4{x^2} + 16x + 15 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x =  - \frac{5}{2} \Rightarrow y =  - \frac{7}{2}}\\{x =  - \frac{3}{2} \Rightarrow y = \frac{3}{2}}\end{array}} \right.} \right.\end{array}\)

Tại \(A\left( { - \frac{5}{2}, - \frac{7}{2}} \right)\) có tiếp tuyến \(\left( {{T_1}} \right):y =  - 3\left( {x + \frac{5}{2}} \right) - \frac{7}{2} \Leftrightarrow y =  - 3x - 11\)

Tại \(B\left( { - \frac{3}{2},\frac{3}{2}} \right)\) có tiếp tuyến \(\left( {{T_2}} \right):y =  - 3\left( {x + \frac{3}{2}} \right) + \frac{3}{2} \Leftrightarrow y =  - 3x - 3\)\[{x^2} + 3x + 3 = m|x + 2| \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne  - 2}\\{\frac{{{x^2} + 3x + 3}}{{\left| {x + 2} \right|}} = m}\end{array}} \right.\]

\( \Rightarrow \)Số giao điểm của đồ thị \(\left( {{C_1}} \right)\)

\(\begin{array}{*{20}{l}}y&{ = \frac{{{x^2} + 3x + 3}}{{|x + 2|}}}\\{}&{ = \left\{ {\begin{array}{*{20}{l}}{\frac{{{x^2} + 3x + 3}}{{x + 2}}}&{{\rm{ (1):  }}x >  - 2}\\{ - \left( {\frac{{{x^2} + 3x + 3}}{{x + 2}}} \right)}&{{\rm{ (2):  }}x <  - 2}\end{array}} \right.}\end{array}\)

(1): bên phải tiệm cận đứng: giữ nguyên \((C)\)

(2): bên trái tiệm cận đứng: lấy đối xứng của \((C)\) qua trục \(Ox\) \(\left( {{C_1}} \right)\) là đường có nét liền, đậm

Số giao điểm của \(\left( {{C_1}} \right)\) và đường thẳng \(y = m\) là số nghiệm của phương trình.

Vị trí của đường thẳng \(y = m\) để có 4 giao điểm với \(\left( {{C_1}} \right)\) là \(m > 3\)