Một công ty bất động sản có \(20\) phòng cho thuê. Biết rằng nếu cho thuê mỗi phòng với giá \(2\) triệu đồng một tháng thì tất cả các phòng đều có người thuê. Nhưng cứ mỗi lần tăng giá cho thuê mỗi phòng thêm \(200\) nghìn đồng một tháng thì có thêm một phòng bị bỏ trống. Hỏi công ty nên cho thuê mỗi phòng bao nhiêu triệu đồng một tháng để tổng số tiền thu được là lớn nhất?
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Cứ tăng thêm \(200\) nghìn đồng vào giá thuê một phòng trên một tháng thì có một phòng bị bỏ trống.
Gọi số lần tăng \(200\) nghìn đồng vào giá thuê một phòng trên một tháng là \[x\left( {x \in {\mathbb{N}^*}} \right)\].
Khi đó \[x\] cũng là số phòng bị bỏ trống.
Tổng số tiền công ty thu được lúc này là:
\[T\left( x \right) = \left( {2000 + 200x} \right)\left( {20 - x} \right) = - 200{x^2} + 2000x + 40000\] .
Xét hàm số \[T\left( x \right) = - 200{x^2} + 2000x + 40000\] với \[x > 0\].
\[\begin{array}{l} \Rightarrow T'\left( x \right) = - 400x + 2000\\T'\left( x \right) = 0\\ \Leftrightarrow - 400x + 2000 = 0\\ \Leftrightarrow x = 5\left( {TM} \right)\end{array}\]
Bảng biến thiên của hàm số \[T\left( x \right)\] như sau:
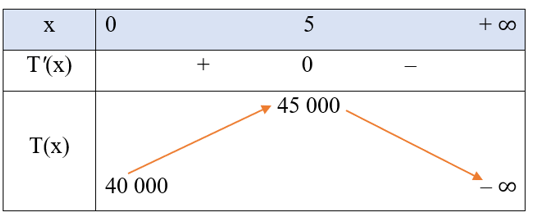
Căn cứ vào bảng biến thiên trên, ta thấy hàm số \[T\left( x \right)\] đạt giá trị lớn nhất bằng 45 000 khi \[x = 5\]
Khi đó, số tiền tăng lên khi cho thuê một phòng là \[200.5 = 1000\] = 1.
Vậy công ty nên cho thuê mỗi căn hộ 3 triệu đồng một tháng thì tổng số tiền thu được là lớn nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(\vec P = m\vec g\) suy ra \(P = mg = 20.10 = 200\left( {{\rm{\;N}}} \right)\).
Vậy trọng lực tác dụng lên em bé là 200 N.
Ta có \(A = P \cdot s \cdot \cos \left( {\vec P,\vec s} \right) = 200 \cdot 2 \cdot \cos {80^ \circ } \approx 69\) (J).
Vậy công sinh bởi trọng lực \(\vec P\) khi em bé trượt hết chiều dài cầu trượt là 306 J.
Lời giải
|
a) |
S |
b) |
Đ |
c) |
S |
d) |
Đ |
(a) Đúng: Áp dụng công thức tính độ dài đoạn thẳng ta tính được
\(AB = CD = \sqrt {10} ;AC = BD = \sqrt {13} ;AD = BC = \sqrt 5 \)
Vậy tứ diện \(ABCD\) có các cạnh đối đôi một bằng nhau
(b) Sai: Ta có: \(\overrightarrow {AB} = \left( { - 1;0;3} \right),\overrightarrow {CD} = \left( { - 1;0; - 3} \right)\). Gọi \(\varphi \) là góc giữa \(AB\) và \(CD\)
\(\cos \varphi = \cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = \frac{{\left| { - 8} \right|}}{{\sqrt {10} .\sqrt {10} }} = \frac{4}{5}\)
Vậy góc giữa \(AB\) và \(CD\) là \(\varphi = \arccos 0,8\)
(c) Sai: Lấy \[I\] trung điểm của \(AB,J\) là trung điểm của \(CD\)
\(\Delta ACD = \Delta BCD\)(c.c.c) nên 2 đường trung tuyến tương ứng \(AJ = BJ\).
Vậy \(\Delta AJB\) cân đỉnh \(J\) nên \[IJ\] vuông góc với \(AB\) tại \(I\).
Tương tự \(\Delta ICD\) cân đỉnh \[I\] nên \[IJ\] vuông góc với \(CD\) tại \(J\).
Vậy \[IJ\] là đường vuông góc chung của \(AB\) và \(CD\) ta được \(I\left( {\frac{3}{2};1;\frac{3}{2}} \right)\) và \(J\left( {\frac{3}{2}; - 1;\frac{3}{2}} \right)\)
Vậy khoảng cách giữa \(AB\) và \(CD\) chính là độ dài đoạn vuông góc chung \(IJ\).
\(d\left( {AB;CD} \right) = II = \sqrt {{{\left( {\frac{3}{2} - \frac{3}{2}} \right)}^2} + {{\left[ {1 - \left( { - 1} \right)} \right]}^2} + {{\left( {\frac{3}{2} - \frac{3}{2}} \right)}^2}} = 2\)
(d) Đúng: Theo kết quả câu 3. Lấy \[G\] là trung điểm của \(IJ\) ta được:
\(GA = GB\)vì \(\Delta GAB\) cân đỉnh \(G\);\(GC = GD\) vì \(\Delta GCD\) cân đỉnh \(G\)
Mà \(GA = \sqrt {G{I^2} + I{A^2}} \) mà \(GI = GJ,IA = ID\) và \(GC = \sqrt {G{J^2} + I{D^2}} \)
Do đó \(GA = GB = GC = GD = R\)
Do đó \[G\]: Tâm mặt cầu ngoại tuyến khối tứ diện \(ABCD:G\left( {\frac{3}{2};0;\frac{3}{2}} \right)\) và bán kính của mặt cầu là \(R = GA = \frac{{\sqrt {14} }}{2}\) (\[G\]: cũng chính là trọng tâm của khối tứ diện gần đều \(ABCD\))
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
