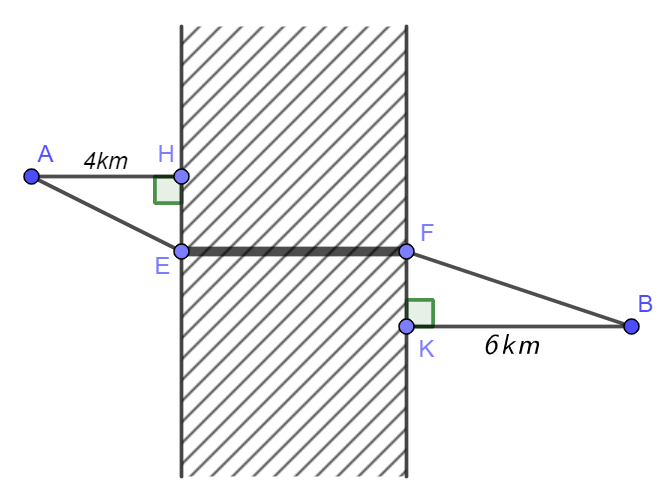
Hai thành phố A và B cách nhau một con sông. Người ta xây dựng một cây cầu \(EF\) bắc qua sông. Biết rằng thành phố \(A\) cách con sông một khoảng là \(4km\) và thành phố \(B\) cách con sông một khoảng là \(6km\)(hình vẽ), biết \(HE + KF = 20km\) và độ dài \(EF\) không đổi. Hỏi xây cây cầu tại vị trí \(E\)cách thành phố \(A\) là bao nhiêu \(km\) để đường đi từ thành phố A đến thành phố B là ngắn nhất (đi theo đường \(AEFB\))? (kết quả làm tròn đến phần trăm).

Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Đặt \[HE = {x_{}}{,_{}}FK = y\], với \[x,\,y > 0\]
Ta có: \[HE + KF = 20 \Rightarrow x + y = 20\], \[\left\{ \begin{array}{l}AE = \sqrt {16 + {x^2}} \\BF = \sqrt {36 + {y^2}} = \sqrt {36 + {{\left( {20 - x} \right)}^2}} \end{array} \right.\]
Nhận xét: Vì \[EF\] không đổi nên \[AB\] ngắn nhất khi \[AE + BF\] nhỏ nhất.
Ta có \[AE + BF\]\[ = \sqrt {{x^2} + 16} + \sqrt {{{(20 - x)}^2} + 36} = \sqrt {{x^2} + 16} + \sqrt {{x^2} - 40x + 436} = f(x)\]
\[f'(x) = \frac{x}{{\sqrt {{x^2} + 16} }} + \frac{{x - 20}}{{\sqrt {{x^2} - 40x + 436} }},\,\forall x \in \left( {0;20} \right)\].
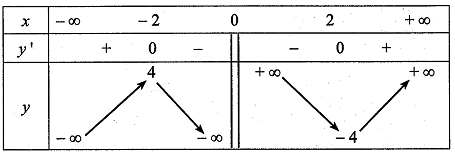
Cho \[f'(x) = 0 \Rightarrow x = 8\]
Bảng biến thiên
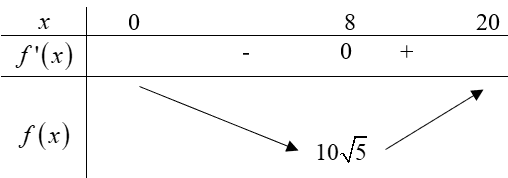
Vậy \(AE = \sqrt {{8^2} + 16} \approx 8,94km\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
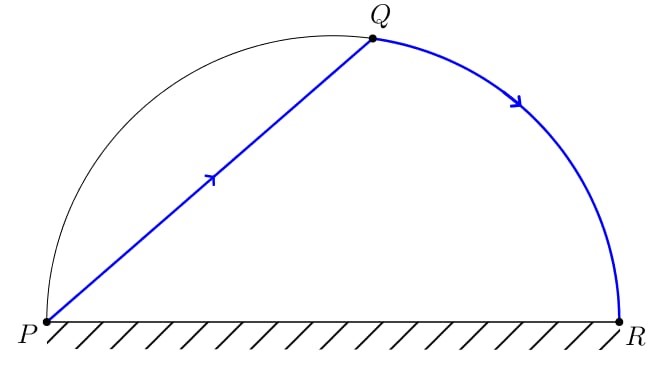
Đặt \(\widehat {QPR} = \varphi \left( {rad} \right)\), \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
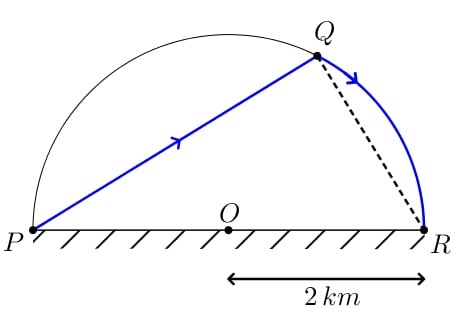
Ta có \(\Delta PQR\) vuông tại \(Q\) \( \Rightarrow PQ = PR.\cos \varphi = 4\cos \varphi \).
Mà \(\widehat {QOR} = 2\widehat {QPR} = 2\varphi \).
Độ dài cung tròn \(QR = 2.2\varphi = 4\varphi \).
Thời gian anh Tài chèo từ \(P\) đến \(Q\) là: \(\frac{{4\cos \varphi }}{3}\) (giờ).
Thời gian anh Tài chèo từ \(Q\) đến \(R\) là: \(\frac{{4\varphi }}{6} = \frac{{2\varphi }}{3}\) (giờ).
Tổng thời gian anh Tài di chuyển từ \(P\) đến \(R\) là: \(t = \frac{{4\cos \varphi }}{3} + \frac{{2\varphi }}{3}\,\,\left( {0 < \varphi < \frac{\pi }{2}} \right)\).
Xét hàm số \(t\left( \varphi \right) = \frac{{4\cos \varphi }}{3} + \frac{{2\varphi }}{3}\) với \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
\(t'\left( \varphi \right) = \frac{1}{3}\left( { - 4\sin \varphi + 2} \right)\), \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
\(t'\left( \varphi \right) = 0,\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\)
\( \Leftrightarrow \sin \varphi = \frac{1}{2},\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\)
\( \Leftrightarrow \varphi = \frac{\pi }{6}\).
Bảng biến thiên
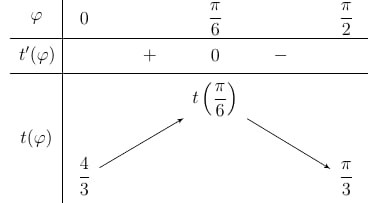
Vậy thời gian chậm nhất mà anh Tài di chuyển từ \(P\) đến \(R\)là \(t\left( {\frac{\pi }{6}} \right) = \frac{{2\sqrt 3 }}{3} + \frac{\pi }{9} \approx 1,5\)(giờ) hay 90 phút.
Lời giải
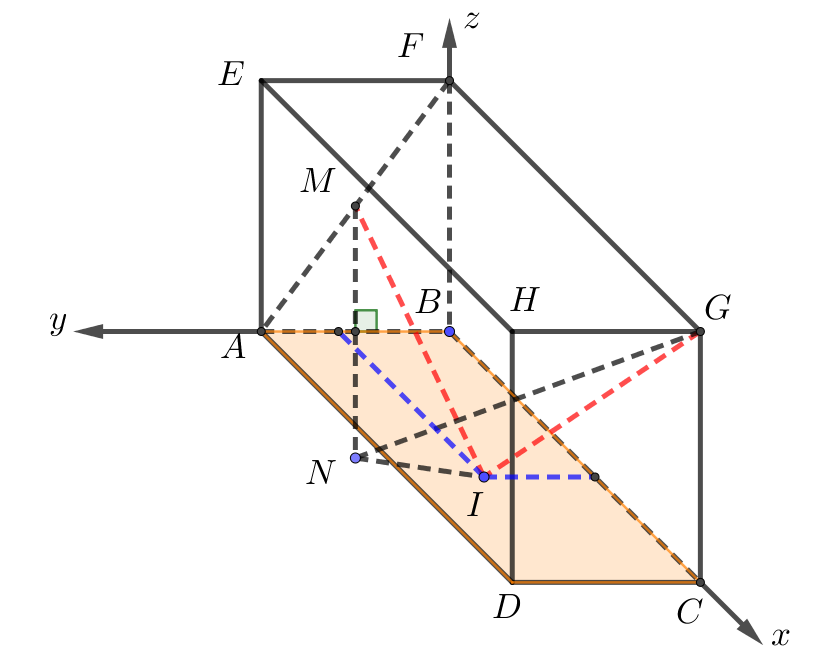
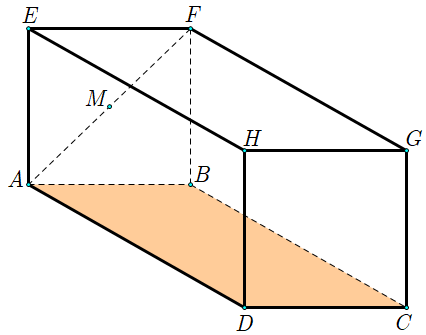
Dựng hệ trục \(Oxyz\) như hình vẽ
Khi đó tọa độ các điểm là \(B\left( {0;\,0;\,0} \right)\), \(C\left( {8;\,0;\,0} \right)\), \(D\left( {8;\,6;\,0} \right)\), \(A\left( {0;\,6;\,0} \right)\), \(G\left( {8;\,0;\,10} \right)\), \(F\left( {0;\,0;\,10} \right)\).
Ta có: \(M\) là trung điểm của \(AF\)\( \Rightarrow M\left( {0;\,3;\,5} \right)\).
Con cá bơi từ điểm \(G\) đến chạm mặt đáy hồ tại điểm \(I\left( {x;\,y;\,0} \right) \in \left( {Oxy} \right)\) với \(0 \le x \le 8\), \(0 \le y \le 6\).
Gọi \(N\) là điểm đối xứng của điểm \(M\) qua \(\left( {Oxy} \right)\) \( \Rightarrow N\left( {0;\,3;\, - 5} \right)\).
Quãng đường di chuyển của con cá là \(G - I - M\)
Ta có: \(IM + IG = IN + IG \ge GN\)\( = \sqrt {{{\left( {0 - 8} \right)}^2} + {{\left( {3 - 0} \right)}^2} + {{\left( { - 5 - 10} \right)}^2}} = \sqrt {298} \).
Để \(IM + IG\) nhỏ nhất thì ba điểm \(I\), \(G\), \(N\) thẳng hàng
Suy ra \(\overrightarrow {IG} \), \(\overrightarrow {NG} \) cùng phương.
\(\overrightarrow {IG} = \left( {8 - x;\, - y;\,10} \right)\).
\(\overrightarrow {NG} = \left( {8;\, - 3;\,15} \right)\).
Do đó \(\frac{{8 - x}}{8} = \frac{{ - y}}{{ - 3}} = \frac{{10}}{{15}}\).
Suy ra \(x = \frac{8}{3}\), \(y = 2\)\( \Rightarrow I\left( {\frac{8}{3};\,2;\,0} \right)\).
Khi đó, \(a = d\left( {I,BA} \right) = \frac{8}{3}\), \(b = d\left( {I,BC} \right) = 2\).
Vậy \(D = 3a + 6b = 3 \cdot \frac{8}{3} + 6 \cdot 2 = 20\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.