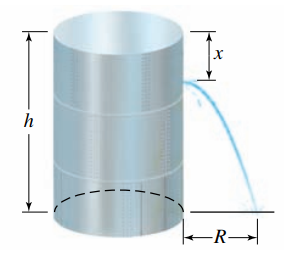
Một bồn hình trụ cao \(h\) chứa nước. Theo định luật Torricelli, vận tốc tia nước chảy qua lỗ ở độ sâu \(x\) so với mặt nước là \(V = \sqrt {2gx} \). Người ta cho rằng tầm xa \(R\) (feet) của tia nước được cho bởi \(R = 2\sqrt {x(h - x)} \)Biết lỗ phun nên đặt ở độ cao \(x = K.h,\,(K \in \mathbb{R})\) so với mặt bồn thì tầm xa \(R\) đạt cực đại. Tìm \(K\)?

Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Thay vì trực tiếp tối đa \(R(x)\), ta có thể tối đa \({R^2}(x)\) (vì hàm căn là tăng):
\({R^2}(x) = 4x(h - x) = 4\left( {hx - {x^2}} \right)\)
Tính đạo hàm: \[{\left( {{R^2}(x)} \right)^\prime } = 4(h - 2x)\]
Giải \({\left( {{R^2}} \right)^\prime } = 0\): \(h - 2x = 0 \Rightarrow x = \frac{h}{2}.\)
Lập bảng biến thiên ta có \(x = \frac{h}{2}\) là điểm cực đại.
Vậy lỗ phun nên đặt ở độ cao \(x = \frac{h}{2}\) để tầm xa \(R\) của tia nước đạt tối đa.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
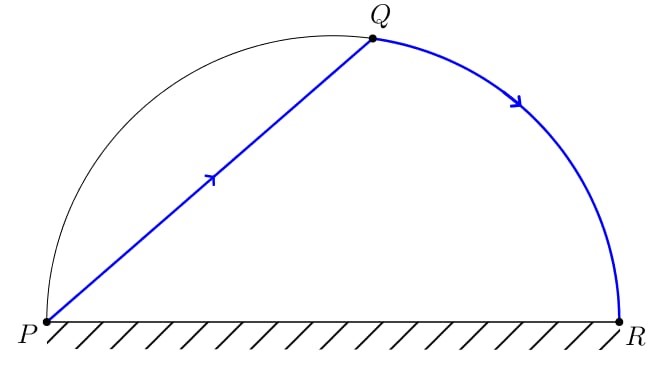
Đặt \(\widehat {QPR} = \varphi \left( {rad} \right)\), \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
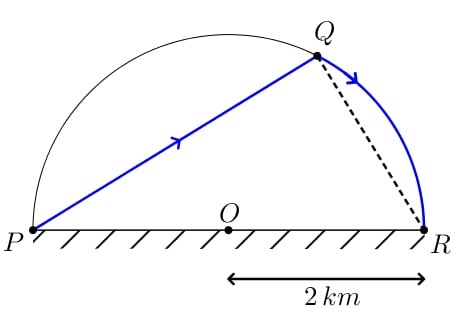
Ta có \(\Delta PQR\) vuông tại \(Q\) \( \Rightarrow PQ = PR.\cos \varphi = 4\cos \varphi \).
Mà \(\widehat {QOR} = 2\widehat {QPR} = 2\varphi \).
Độ dài cung tròn \(QR = 2.2\varphi = 4\varphi \).
Thời gian anh Tài chèo từ \(P\) đến \(Q\) là: \(\frac{{4\cos \varphi }}{3}\) (giờ).
Thời gian anh Tài chèo từ \(Q\) đến \(R\) là: \(\frac{{4\varphi }}{6} = \frac{{2\varphi }}{3}\) (giờ).
Tổng thời gian anh Tài di chuyển từ \(P\) đến \(R\) là: \(t = \frac{{4\cos \varphi }}{3} + \frac{{2\varphi }}{3}\,\,\left( {0 < \varphi < \frac{\pi }{2}} \right)\).
Xét hàm số \(t\left( \varphi \right) = \frac{{4\cos \varphi }}{3} + \frac{{2\varphi }}{3}\) với \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
\(t'\left( \varphi \right) = \frac{1}{3}\left( { - 4\sin \varphi + 2} \right)\), \(\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\).
\(t'\left( \varphi \right) = 0,\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\)
\( \Leftrightarrow \sin \varphi = \frac{1}{2},\,\,\varphi \in \left( {0\,;\,\,\frac{\pi }{2}} \right)\)
\( \Leftrightarrow \varphi = \frac{\pi }{6}\).
Bảng biến thiên
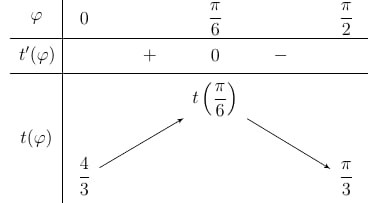
Vậy thời gian chậm nhất mà anh Tài di chuyển từ \(P\) đến \(R\)là \(t\left( {\frac{\pi }{6}} \right) = \frac{{2\sqrt 3 }}{3} + \frac{\pi }{9} \approx 1,5\)(giờ) hay 90 phút.
Lời giải
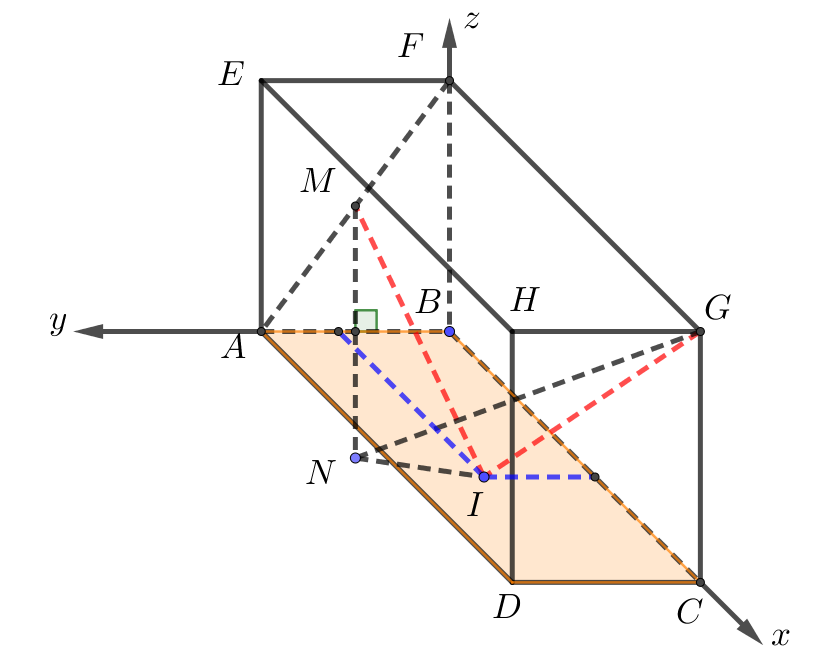
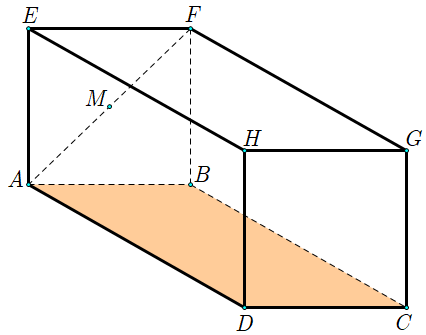
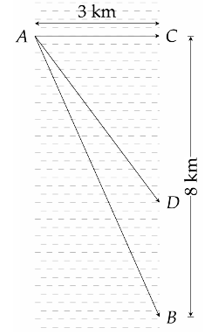
Dựng hệ trục \(Oxyz\) như hình vẽ
Khi đó tọa độ các điểm là \(B\left( {0;\,0;\,0} \right)\), \(C\left( {8;\,0;\,0} \right)\), \(D\left( {8;\,6;\,0} \right)\), \(A\left( {0;\,6;\,0} \right)\), \(G\left( {8;\,0;\,10} \right)\), \(F\left( {0;\,0;\,10} \right)\).
Ta có: \(M\) là trung điểm của \(AF\)\( \Rightarrow M\left( {0;\,3;\,5} \right)\).
Con cá bơi từ điểm \(G\) đến chạm mặt đáy hồ tại điểm \(I\left( {x;\,y;\,0} \right) \in \left( {Oxy} \right)\) với \(0 \le x \le 8\), \(0 \le y \le 6\).
Gọi \(N\) là điểm đối xứng của điểm \(M\) qua \(\left( {Oxy} \right)\) \( \Rightarrow N\left( {0;\,3;\, - 5} \right)\).
Quãng đường di chuyển của con cá là \(G - I - M\)
Ta có: \(IM + IG = IN + IG \ge GN\)\( = \sqrt {{{\left( {0 - 8} \right)}^2} + {{\left( {3 - 0} \right)}^2} + {{\left( { - 5 - 10} \right)}^2}} = \sqrt {298} \).
Để \(IM + IG\) nhỏ nhất thì ba điểm \(I\), \(G\), \(N\) thẳng hàng
Suy ra \(\overrightarrow {IG} \), \(\overrightarrow {NG} \) cùng phương.
\(\overrightarrow {IG} = \left( {8 - x;\, - y;\,10} \right)\).
\(\overrightarrow {NG} = \left( {8;\, - 3;\,15} \right)\).
Do đó \(\frac{{8 - x}}{8} = \frac{{ - y}}{{ - 3}} = \frac{{10}}{{15}}\).
Suy ra \(x = \frac{8}{3}\), \(y = 2\)\( \Rightarrow I\left( {\frac{8}{3};\,2;\,0} \right)\).
Khi đó, \(a = d\left( {I,BA} \right) = \frac{8}{3}\), \(b = d\left( {I,BC} \right) = 2\).
Vậy \(D = 3a + 6b = 3 \cdot \frac{8}{3} + 6 \cdot 2 = 20\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.