Cho hàm số \(y = {x^3} - m{x^2} - \left( {m - 6} \right)x + 1\)(tham số \[m\]). Khi đó:
a) Để hàm số đồng biến trên khoảng \(\left( {0;4} \right)\) thì \(m \le 2\)
b) Với \(m = 6\) thì hàm số đồng biến trên khoảng \(\left( {4; + \infty } \right)\)
c) Với \(m = 0\) thì hàm số nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)
d) Tập hợp tất cả các giá trị của tham số\(m\) để hàm số đồng biến trên khoảng \(\left( {0;4} \right)\) là \(\left( { - \infty ;a} \right]\). Khi đó \(\mathop {\lim }\limits_{x \to a} \left( {x + 2024} \right) = 2027\)
Cho hàm số \(y = {x^3} - m{x^2} - \left( {m - 6} \right)x + 1\)(tham số \[m\]). Khi đó:
a) Để hàm số đồng biến trên khoảng \(\left( {0;4} \right)\) thì \(m \le 2\)
b) Với \(m = 6\) thì hàm số đồng biến trên khoảng \(\left( {4; + \infty } \right)\)
c) Với \(m = 0\) thì hàm số nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)
d) Tập hợp tất cả các giá trị của tham số\(m\) để hàm số đồng biến trên khoảng \(\left( {0;4} \right)\) là \(\left( { - \infty ;a} \right]\). Khi đó \(\mathop {\lim }\limits_{x \to a} \left( {x + 2024} \right) = 2027\)
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
|
a) |
S |
b) |
Đ |
c) |
S |
d) |
Đ |
\(y' = 3{x^2} - 2mx - \left( {m - 6} \right)\). Để hàm số đồng biến trên khoảng \(\left( {0;4} \right)\)thì:\(y' \ge 0\),\(\forall x \in \left( {0;4} \right)\).
tức là \(3{x^2} - 2mx - \left( {m - 6} \right) \ge 0\,\,\forall x \in \left( {0;4} \right)\)\( \Leftrightarrow \frac{{3{x^2} + 6}}{{2x + 1}} \ge m\,\forall x \in \left( {0;4} \right)\)
Xét hàm số \(g\left( x \right) = \frac{{3{x^2} + 6}}{{2x + 1}}\) trên \(\left( {0;4} \right)\).
\(g'\left( x \right) = \frac{{6{x^2} + 6x - 12}}{{{{\left( {2x + 1} \right)}^2}}}\),\(\,g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left( {0;4} \right)\\x = - 2 \notin \left( {0;4} \right)\end{array} \right.\)
Ta có bảng biến thiên:
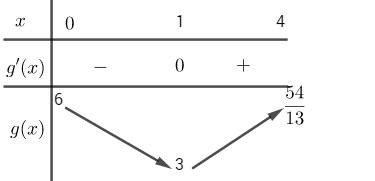
Vậy để \(g\left( x \right) = \frac{{3{x^2} + 6}}{{2x + 1}} \ge m\,\,\forall x \in \left( {0;4} \right)\)thì \(m \le 3\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
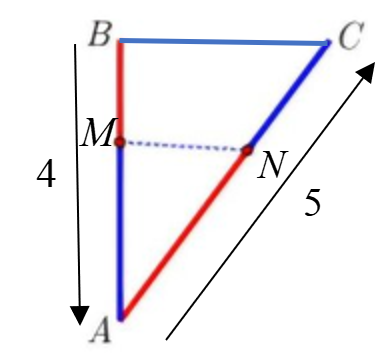
Gọi \(x\)(phút) là khoảng thời gian cả hai chuỗi led đồng thời xuất phát đến \(M\) và \(N\) là hai điểm sáng đầu tiên
\( \Rightarrow \left\{ \begin{array}{l}BM = 4x\\AN = 10x\end{array} \right.\)\( \Rightarrow AM = 4 - 4x\)với \(0 \le x \le 4\)
Xét tam giác \(ABC\) vuông tại \(B\) \( \Rightarrow \cos \widehat {MAN} = \frac{{AB}}{{AC}} = \frac{4}{5}\)
Xét tam giác \(AMN\) ta có : \(M{N^2} = A{M^2} + A{N^2} - 2AM.AN.\cos \widehat {MAN}\)
\(M{N^2} = {\left( {4 - 4x} \right)^2} + {\left( {10x} \right)^2} - 2.\left( {4 - 4x} \right).10x.\frac{4}{5}\)\( = 180{x^2} - 96x + 16 = f\left( x \right)\)
Để khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led nhỏ nhất \( \Leftrightarrow M{N_{\min }} \Leftrightarrow M{N^2}_{\min }\)
Xét \(f\left( x \right) = 180{x^2} - 96x + 16\) với \(x \in \left[ {0;4} \right]\)
\(f'\left( x \right) = 360x - 96 = 0 \Leftrightarrow \)\(x = \frac{4}{{15}}\)\( \Rightarrow M{N^2}\)đạt giá trị nhỏ nhất \( \Leftrightarrow x = \frac{4}{{15}}\) (phút) \( = 16\) (giây)
Vậy sau 16 giây thì hai điểm sáng đầu tiên của chuỗi led có khoảng cách nhỏ nhất.
Lời giải
|
a) |
Đ |
b) |
S |
c) |
Đ |
d) |
Đ |
Ta có
\(\overrightarrow {AB} = \left( {1;0;1} \right),\,\overrightarrow {AC} = \left( { - 3;0;4} \right)\), \(\overrightarrow {AB} \ne k\,\overrightarrow {AC} = \left( { - 3k;0;4k} \right)\) với mọi \(k\)nên hai véctơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)không cùng phương, dó đó ba điểm \(A,\,B,\,C\)không thẳng hàng.
(b) Đúng.
Ta có
\[\overrightarrow {AB} = \left( {1;0;1} \right),\,\overrightarrow {AD} = \left( {2;0;2} \right) \Rightarrow \overrightarrow {AD} = 2\overrightarrow {AB} \], dó đó ba điểm \(A,\,B,\,D\) thẳng hàng.
(c) Sai.
Ta có
\[\overrightarrow {BA} = \left( { - 1;0; - 1} \right),\,\overrightarrow {BC} = \left( { - 4;0;3} \right) \Rightarrow \cos \widehat {ABC} = \cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{1}{{5\sqrt 2 }} \Rightarrow \widehat {ABC} \approx 82^\circ \]
(d) Đúng.
Ta có
\[\overrightarrow {AB} = \left( {1;0;1} \right),\,\overrightarrow {AC} = \left( { - 3;0;4} \right) \Rightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0.4 + 0.1;1.\left( { - 3} \right) - 1.4;1.0 + 0.\left( { - 3} \right)} \right) = \left( {0; - 7;0} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
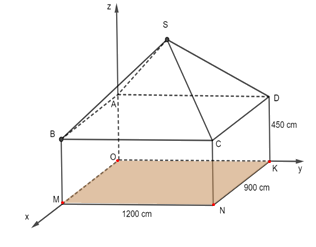
Một ngôi nhà gồm hai phần. Phần thân nhà dạng hình hộp chữ nhật ABCD.OMNK có chiều dài \(1200cm\), chiều rộng \(900cm\), chiều cao\(450cm\). Phần mái nhà dạng hình chóp\(S.ABCD\) có các cạnh bên bằng nhau và tạo với mặt đáy góc \(\alpha \)với \(\tan \alpha = \frac{1}{5}\). Chọn hệ trục toạ độ \(Oxyz\)sao cho \(M\)thuộc tia \(Ox,\)\(K\)thuộc tia \(Oy,\)\(A\)thuộc tia \(Oz\)(như hình vẽ). Biết \(S\left( {a;b;c} \right)\) (đơn vị của \(a,b,c\)là centimet). Tính giá trị của biểu thức \(P = a + b + c.\)

Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.