Tìm \(a\) để giá trị lớn nhất của hàm số \(y = {x^3} - 3a{x^2} + a - 1\) trên đoạn \(\left[ { - 1;a} \right]\) bằng 10, biết \(a > 0\).
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Ta có \(y' = 3{x^2} - 6ax = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2a\end{array} \right.\)
Khi đó bảng biến thiên của hàm số trên đoạn \(\left[ { - 1;a} \right]\)
![Tìm \(a\) để giá trị lớn nhất của hàm số \(y = {x^3} - 3a{x^2} + a - 1\) trên đoạn \(\left[ { - 1;a} \right]\) bằng 10, biết \(a > 0\). A. \(a = 11\). B. \(a = \frac{5}{2}\). C. \(a = \frac{3}{2}\). D. \(a = 10\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/18-1761646953.png)
Từ bảng biến thiên của hàm số ta được \(\mathop {\max }\limits_{\left[ { - 1;a} \right]} y = 10 = y(0) = a - 1 \Rightarrow a = 11.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Theo đề bài ta có : \(OA = 2\,\,{\rm{km}}\), \(OB = 3\,\,{\rm{km}}\) và \[528\,\,{\rm{m = 0,528}}\,\,{\rm{km}}\].
Đồ thị hàm số \[y = f\left( x \right)\] đi qua các điểm \(O\left( {0\,;\,\,0} \right)\), \(A\left( {2\,;\,\,0} \right)\,,\,\,C\left( {3\,;\,\,0} \right)\) suy ra\(y = f\left( x \right) = ax\left( {x - 2} \right)\left( {x - 3} \right) = a\left( {{x^3} - 5{x^2} + 6x} \right)\) với \(a > 0\).
Ta có : \(y' = a\left( {3{x^2} - 10x + 6} \right)\), \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5 + \sqrt 7 }}{3}\\x = \frac{{5 - \sqrt 7 }}{3}\end{array} \right.\).
Từ độ cao của đồi ta có tại vị trí điểm cực đại suy ra \(a = \frac{{0,528}}{{{{\left( {\frac{{5 - \sqrt 7 }}{3}} \right)}^3} - 5.{{\left( {\frac{{5 - \sqrt 7 }}{3}} \right)}^2} + 6.\left( {\frac{{5 - \sqrt 7 }}{3}} \right)}} \approx 0,25\).
Điểm sâu nhất của hồ ứng với vị trí của điểm cực tiểu \({x_{CT}} = \frac{{5 + \sqrt 7 }}{3}\,,\,\,{y_{CT}} \approx 0,1578\).
Vậy độ sâu của hồ tại điểm sâu nhất xấp xỉ \(0,1578\,\,{\rm{km}}\) hay xấp xỉ \(158\,\,{\rm{m}}\).
Lời giải
Nước muối tinh khiết: \(30.40.{\kern 1pt} {\kern 1pt} t{\kern 1pt} \,\) (gam).
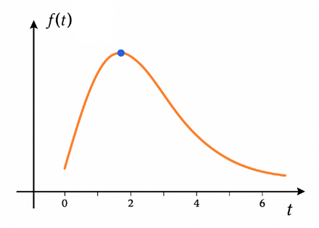
Nồng độ muối sau \(t\) phút: \(f\left( t \right) = \frac{{30.40.t}}{{30t + 3000}}\)
Khi t càng lớn: \(\mathop {\lim }\limits_{x \to + \infty } f\left( t \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{30.40.{\kern 1pt} {\kern 1pt} t}}{{30t + 3000}} = 40\)(gam/lít)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Lát cắt ngang của một vùng đất ven biển được mô hình hoá thành một hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ (đơn vị độ dài trên các trục là km). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/3-1761647380.jpg)