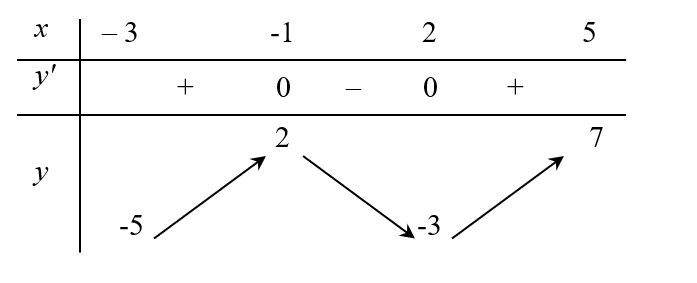
Một giáo viên theo dõi sự tiến bộ của học sinh qua thang đo điểm, được mô hình hóa bằng hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) với \(a,b,c\) là các hệ số. Trong đó \(x\;\left( {0 \le x \le 9,x \in \mathbb{N}} \right)\) là số tháng kể từ đầu năm học và \(f\left( x \right)\) là điểm trong tháng thứ \(x\). Qua theo dõi, giáo viên ghi nhận tháng đầu tiên học sinh đạt 19 điểm, sau đó giảm trong tháng thứ hai và đến tháng thứ ba học sinh đạt mức điểm thấp nhất trong năm học là 3 điểm. Kể từ tháng thứ ba trở đi, điểm của học sinh tăng lên. Tính điểm của học sinh đó ở tháng thứ sáu.

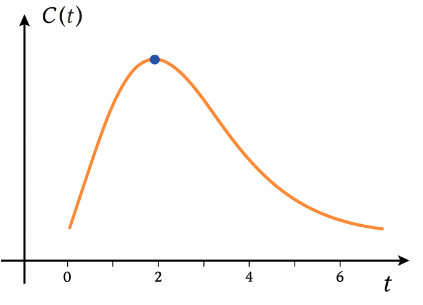
Tốc độ tăng trưởng của virut được tính theo hàm số \(y = p'\left( t \right) = \frac{{1120.{{\rm{e}}^{0,2t}}}}{{{{\left( {{{\rm{e}}^{0,2t}} + 7} \right)}^2}}}\), \(t \ge 0\).

Xét hàm số \(y = g\left( t \right) = \frac{{1120.{{\rm{e}}^{0,2t}}}}{{{{\left( {{{\rm{e}}^{0,2t}} + 7} \right)}^2}}}\), có \(g'\left( t \right) = \frac{{224.{{\rm{e}}^{0,2t}}\left( {7 - {{\rm{e}}^{0,2t}}} \right)}}{{{{\left( {{{\rm{e}}^{0,2t}} + 7} \right)}^3}}}\).

\(g'\left( t \right) = 0 \Leftrightarrow 7 - {e^{0,2t}} = 0 \Leftrightarrow t = 5\ln 7 \approx 9,7\).

Ta có bảng dấu của \(g'\left( t \right)\) như sau:

Dựa vào bảng trên ta thấy tốc độ tăng trưởng của virut sẽ đạt lớn nhất ở ngày thứ 10.

Đăt \(OA = x \Rightarrow AB = 2x\) (\(0 < x < 5\)).

\( \Rightarrow AD = \sqrt {O{D^2} - O{A^2}}  = \sqrt {25 - {x^2}} \).

Diện tích hình chữ nhật \(ABC{\rm{D}}\) là \(S = AB.AD = 2x\sqrt {25 - {x^2}} \).

Xét hàm số: \(f\left( x \right) = 2x\sqrt {25 - {x^2}} \) trên \(\left( {0;5} \right)\), ta có

\(f'\left( x \right) = 2\sqrt {25 - {x^2}}  - \frac{{2{x^2}}}{{\sqrt {25 - {x^2}} }}\).

\(f'\left( x \right) = 0 \Leftrightarrow \frac{{50 - 4{x^2}}}{{\sqrt {25 - {x^2}} }} = 0 \Leftrightarrow 50 - 4{x^2} = 0 \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{5\sqrt 2 }}{2} \in (0;5)}\\{x = \frac{{ - 5\sqrt 2 }}{2} \notin (0;5)}\end{array}} \right.\).

Bảng biến thiên

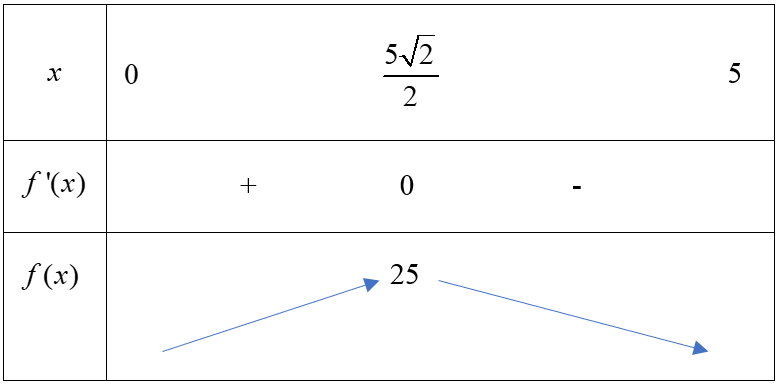
Vậy diện tích lớn nhất của tấm nhôm hình chữa nhật là \(S = 25\) khi \(x = \frac{{5\sqrt 2 }}{2}\).