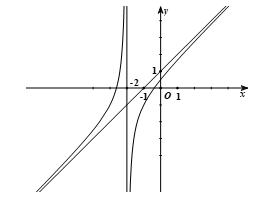
Cho hàm số \(f\left( x \right) = \frac{1}{2}{x^2} + x - 6{\rm{ln}}\left( {x + 2} \right)\).

a) Đạo hàm của hàm số là \(f'\left( x \right) = x + 1 - \frac{6}{{x + 2}}\).

b) Trên đoạn \(\left[ { - 1;2} \right]\), phương trình \(f'\left( x \right) = 0\) có hai nghiệm phân biệt.

c) \(f\left( { - 1} \right) = - \frac{1}{2}\) và \(f\left( 2 \right) = 4 - 12{\rm{ln}}2\).

d) Giá trị nhỏ nhất của \(f\left( x \right)\) trên đoạn \(\left[ { - 1;2} \right]\) lớn hơn –5.

a) Sai. Nếu \[y\] là hàm số biểu thị cho chuyển động của hạt thì \[y'\] là hàm vận tốc \(v\).

b) Đúng. Ta có \[y = {t^3} - 12t + 3 \Rightarrow v = y' = 3{t^2} - 12\].

c) Sai. Dựa vào hàm vận tốc \[v\left( t \right) = 3{t^2} - 12\] thì hạt đi lên khi \(v > 0\) và xuống khi \(v < 0\).

Do đó, vật đi lên khi \(t \in \left( {2; + \infty } \right)\) và đi xuống khi \(t \in \left( {0;2} \right)\).

Vậy tại thời điểm \[t = 1\] thì hạt đang chuyển động đi xuống.

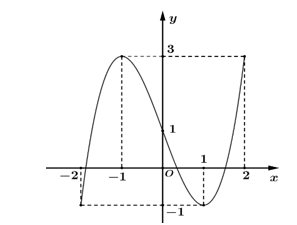
d) Đúng. Từ \[t = 0\] tới \[t = 2\], vật chuyển động từ tọa độ \[y = 3\] đến tọa độ \[y = - 13\], tức là vật đi được quãng đường \[16\] đơn vị độ dài, tương ứng 16 m.

Từ \[t = 2\] tới \[t = 3\], vật chuyển động từ tọa độ \[y = - 13\] đến tọa độ \[y = - 6\], tức là vật đi được quãng đường \[7\] đơn vị độ dài, tương ứng 7 m.

Kết luận quãng đường vật di chuyển trong khoảng thời gian \[0 \le t \le 3\] là \[23\] m.

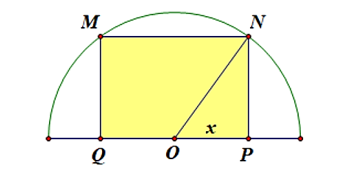
Gọi hình chữ nhật cần tính diện tích là \(MNPQ\) có \(OP = x\)\[\left( {0 < x < 4} \right)\], \(ON = 4\).

Khi đó diện tích của hình chữ nhật \(MNPQ\) là: \[S = MN \cdot NP\]\[ = 2x\sqrt {16 - {x^2}} \].

Xét hàm số \[f\left( x \right) = 2x\sqrt {16 - {x^2}} \]trên \[\left( {0;\,4} \right)\].

Ta có \(f'\left( x \right) = 2\sqrt {16 - {x^2}} - \frac{{2{x^2}}}{{\sqrt {16 - {x^2}} }}\)\( = \frac{{ - 4{x^2} + 32}}{{\sqrt {16 - {x^2}} }}\); \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\sqrt 2 \in \left( {0;\,4} \right)\\x = - 2\sqrt 2 \notin \left( {0;\,4} \right)\end{array} \right.\).

Bảng biến thiên:

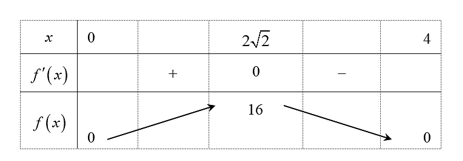
Ta có \(\mathop {\max }\limits_{\left( {0;\,4} \right)} f\left( x \right) = f\left( {2\sqrt 2 } \right) = 16\).

Vậy diện tích lớn nhất của hình chữ nhật có thể cắt được là \(16\,{\rm{(d}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\).

Đáp án: 16.