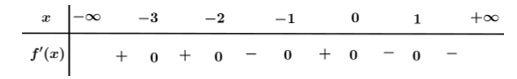Đề ôn luyện Toán Chương 1. Ứng dụng đạo hàm để khảo sát hàm số (đề số 2)
35 người thi tuần này 4.6 1.3 K lượt thi 22 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
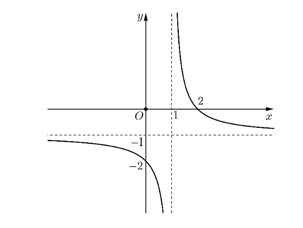
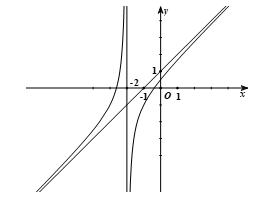
A. Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
B. Hàm số nghịch biến trên \(\mathbb{R}\).
C. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
D. Hàm số đồng biến trên \(\mathbb{R}\).
Lời giải
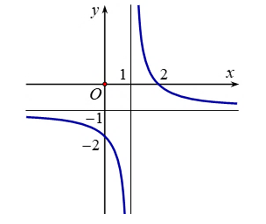
Đồ thị hàm số \(y\, = \,f\left( x \right)\) đi xuống từ trái qua phải và nhận đường thẳng \(x\, = \,1\) làm tiệm cận đứng.
Do đó, hàm số \(y\, = \,f\left( x \right)\) nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\). Chọn C.
Câu 2
A. \(x = 7\).
B. \(x = - 2\).
C. \(x = 0\).
D. \(x = 6\).
Lời giải
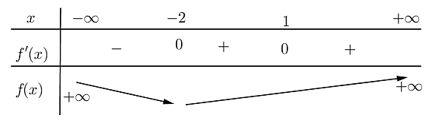
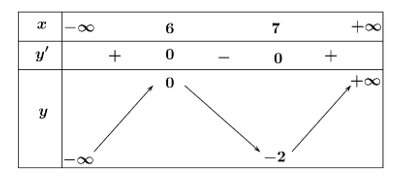
Quan sát bảng biến thiên, ta thấy điểm cực đại của hàm số \(y = f\left( x \right)\) là \(x = 6\). Chọn D.
Câu 3
Lời giải
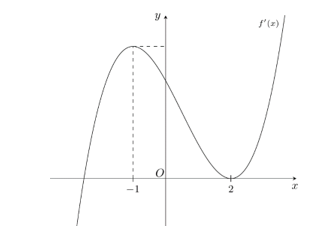
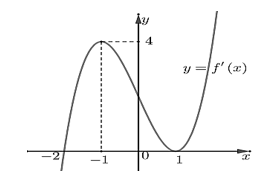
Dựa vào đồ thị ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 1\end{array} \right.\).
Ta có bảng biến thiên của hàm số \(y = f\left( x \right)\):
Vậy hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - 2; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
Vậy phương án C sai. Chọn C.
Câu 4
Lời giải
Ta có \[y' = - 3{x^2} + 6x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\].
Hàm số đồng biến khi \(y' > 0\)\( \Leftrightarrow 0 < x < 2\). Chọn D.
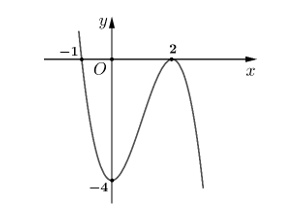
Câu 5
A. \[x = 1\].
B. \[x = - 2\].
C. \[M\left( {1\,;\, - 2} \right)\].
D. \[M\left( { - 2\,;\, - 4} \right)\].
Lời giải
Dựa vào đồ thị hàm số ta thấy điểm cực tiểu của đồ thị hàm số \(y = f\left( x \right)\) là \[M\left( {1\,;\, - 2} \right)\]. Chọn C.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
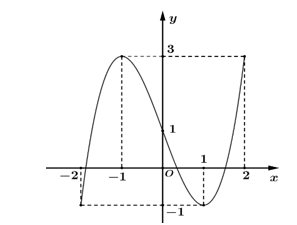
A. \[y = - {x^3} + 3{x^2} - 4.\]
B. \[y = {x^3} - 4.\]
C. \[y = {x^2} - 4.\]
D. \[y = - {x^2} - 4.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số y = f(x) xác định và liên tục trên đoạn [ -2; 2] và có đồ thị là đường cong trong hình vẽ sau (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/blobid0-1762223692.png)