Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là \(27\) (triệu đồng) và bán ra với giá là \(31\) triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là \(600\) chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm \(1\) triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm \(200\) chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu triệu đồng để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất?
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là \(27\) (triệu đồng) và bán ra với giá là \(31\) triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là \(600\) chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm \(1\) triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm \(200\) chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu triệu đồng để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trả lời: 30,5
Gọi \(x\) (triệu) đồng là số tiền mà doanh nghiệp A dự định giảm giá; \(\left( {0 \le x \le 4} \right)\).
Khi đó:
Lợi nhuận thu được khi bán một chiếc xe là \(31 - x - 27\)\( = 4 - x\) (triệu đồng).
Số xe mà doanh nghiệp sẽ bán được trong một năm là \(600 + 200x\) (chiếc).
Lợi nhuận mà doanh nghiệp thu được trong một năm là
\(f\left( x \right) = \left( {4 - x} \right)\left( {600 + 200x} \right)\)\( = - 200{x^2} + 200x + 2400\).
Xét hàm số \(f\left( x \right) = - 200{x^2} + 200x + 2400\) trên đoạn \(\left[ {0;4} \right]\) có bảng biến thiên
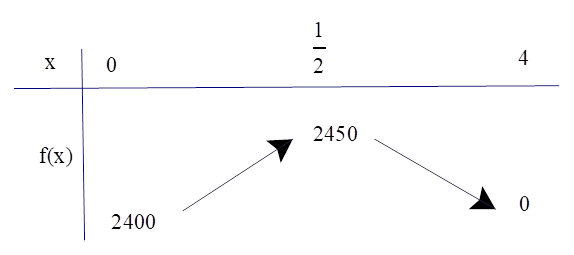
Vậy \(\mathop {\max }\limits_{\left[ {0;4} \right]} f\left( x \right) = 2\,450\)\( \Leftrightarrow x = \frac{1}{2}\).
Vậy giá mới của chiếc xe là \(30,5\) triệu đồng thì lợi nhuận thu được là cao nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Trả lời: 1
Gọi \(x\) là số bàn tiệc thực tế trong đám cưới ( \(x\) nguyên dương và \(x \in [30;35]\) ) và \(y\) (triệu đồng) là số tiền mà người đó phải trả cho nhà hàng.
Nếu đăng ký tại nhà hàng thứ nhất, người đó sẽ trả tiền theo công thức: \(y = 2x + 20\).
Với \(x \in [30;35]\) thì \(y \in [80;90]\), tức là người đó phải trả khoản tiền khoảng 80 triệu đến 90 triệu cho nhà hàng thứ nhất.
Nếu đăng ký tại nhà hàng thứ hai, người đó sẽ trả tiền theo công thức: \(y = 2,5x + 10\).
Với \(x \in [30;35]\) thì \(y \in [85;97,5]\), tức là người đó phải trả khoản tiền khoảng 85 triệu đến 97,5 triệu cho nhà hàng thứ hai.
Vậy, nếu chất lượng phục vụ hai nhà hàng là tương đương, người đó nên chọn nhà hàng thứ nhất để tiết kiệm một khoản chi phí tiệc cưới.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Trả lời: 26,4
Trong tam giác vuông \(DAC\) ta có
\[AC = \frac{{DC}}{{\cos \widehat {ACD}}} = \frac{{18}}{{\cos 40^\circ }} \approx 23,5\left( {\rm{m}} \right)\].
\(AD = DC.\tan \widehat {ACD} = 18.\tan 40^\circ \approx 15,1\left( {\rm{m}} \right)\).
Vậy chiều cao tòa nhà: \(AE = AD + DE = 15,1 + 5 = 20,1\left( {\rm{m}} \right)\).
Trong tam giác vuông \(BCD\), ta có \(BC = \frac{{DC}}{{\cos \widehat {BCD}}} = \frac{{18}}{{\cos 50^\circ }} \approx 28\left( {\rm{m}} \right)\).
Mặt khác, ta có \(\widehat {BCA} = \widehat {BC{\rm{D}}} - \widehat {AC{\rm{D}}} = 10^\circ \), do đó ta có:
\(AB = \sqrt {A{C^2} + B{C^2} - 2AC.BC.\cos \widehat {BCA}} = \sqrt {{{23,5}^2} + {{28}^2} - 2.23,5.28.\cos 10^\circ } \approx 6,3\left( {\rm{m}} \right)\).
Chiều cao cột cờ: \(6,3{\rm{(m)}}\)
Vậy tổng chiều cao của tòa nhà và cột cờ là \(20,1 + 6,3 = 26,4\left( {\rm{m}} \right)\).
Câu 3
A. \(y = {x^2} - 3x + 1\).
B. \(y = 2{x^2} - 3x + 1\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AM} \).
B. \(\overrightarrow {AG} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(y = {x^2} + 4x\)
B. \(y = - {x^2} - 4x - 8\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập