Cho hình vẽ:
Khi đó:
Quảng cáo
Trả lời:
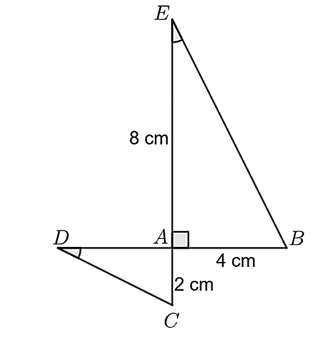
a) Sai.
Vì tam giác \(AEB\) vuông tại \(A\) nên theo định lý Pythagore ta có:
\(E{B^2} = A{B^2} + A{E^2} = {8^2} + {4^2} = 80\) nên \(EB = \sqrt {80} \approx 8,9\;{\rm{cm}}{\rm{.}}\)
Vậy \(EB < 10\;{\rm{cm}}{\rm{.}}\)
b) Đúng.
\(\Delta AEB\) và \(\Delta ADC\) có: \(\widehat {EAB} = \widehat {DAC} = 90^\circ ,\;\,\widehat E = \widehat D\) nên \(\Delta AEB \sim \Delta ADC\) (g.g).
c) Đúng.
Vì \(\Delta AEB \sim \Delta ADC\) nên \(\frac{{AE}}{{AD}} = \frac{{EB}}{{DC}} = \frac{{AB}}{{AC}} = \frac{4}{2} = 2.\) Vậy \(EB = 2DC.\)
d) Sai.
Ta có: \(DC = \frac{{EB}}{2} \approx 4,5\;\,\left( {{\rm{cm}}} \right);\;\,\frac{{AE}}{{AD}} = 2\) nên \(AD = \frac{{AE}}{2} = \frac{8}{2} = 4\;\,\left( {{\rm{cm}}} \right).\)
Chu vi \(\Delta ADC\) là: \(AC + AD + DC = 2 + 4 + 4,5 = 10,5\;\,\left( {{\rm{cm}}} \right).\)
Vậy chu vi \(\Delta ADC\) nhỏ hơn \(15\;{\rm{cm}}{\rm{.}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
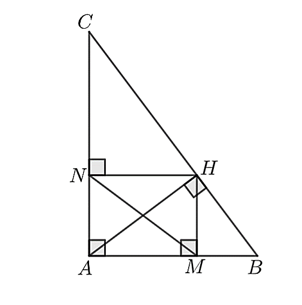
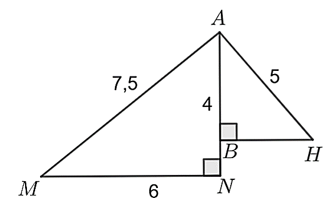
a) Đúng.
Vì \(M,\;\,N\) lần lượt là hình chiếu của \(H\) trên \(AB,\;\,AC\) nên \(HM \bot AB;\;\,HN \bot AC.\)
Do đó, \(\widehat {AMH} = \widehat {HMB} = \widehat {ANH} = \widehat {HNC} = 90^\circ .\)
Vì \(AH\) là đường cao của tam giác \(ABC\) nên \(AH \bot BC.\) Suy ra \(\widehat {AHB} = \widehat {AHC} = 90^\circ .\)
\(\Delta AHM\) và \(\Delta ABH\) có: \(\widehat {AMH} = \widehat {AHB} = 90^\circ ;\;\,\widehat {HAM}\) chung nên \(\Delta AHM \sim \Delta ABH\) (g.g).
b) Đúng.
\(\Delta AHN\) và \(\Delta ACH\) có: \(\widehat {ANH} = \widehat {AHC} = 90^\circ ;\;\,\widehat {HAN}\) chung nên \(\Delta AHN \sim \Delta ACH\) (g.g).
Do đó, \(\frac{{AH}}{{AC}} = \frac{{AN}}{{AH}}.\) Suy ra \(A{H^2} = AN \cdot AC.\)
c) Sai.
Theo a) ta có: \(\Delta AHM \sim \Delta ABH\) (g.g) nên \(\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}.\) Suy ra \(AM \cdot AB = A{H^2}.\)
Mà \(A{H^2} = AN \cdot AC\) nên \(AM \cdot AB = AN \cdot AC.\)
d) Đúng.
Vì \(AM \cdot AB = AN \cdot AC\) nên \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}.\)
\(\Delta ANM\) và \(\Delta ABC\) có: \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}};\;\,\widehat {NAM} = \widehat {BAC} = 90^\circ \) chung nên \(\Delta ANM \sim \Delta ABC\)(c.g.c).
Lời giải
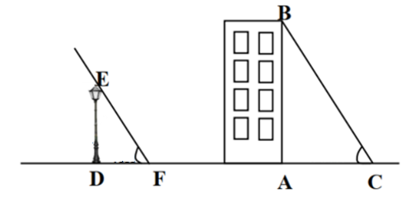
Đáp án: \(2,8\)
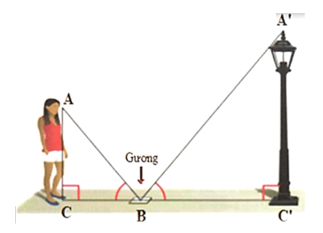
\(\Delta BCA\) và \(\Delta BC'A'\) có: \(\widehat {ACB} = \widehat {BC'A'} = 90^\circ ;\;\,\widehat {ABC} = \widehat {A'BC'}\) nên \(\Delta BCA \sim \Delta BC'A'\) (g.g).
Do đó, \(\frac{{BC}}{{BC'}} = \frac{{AC}}{{A'C'}}\) suy ra \(A'C' = \frac{{AC \cdot BC'}}{{BC}} = \frac{{1,5 \cdot 1,4}}{{0,75}} = 2,8\;\,\left( {\rm{m}} \right).\)
Vậy chiều cao cột đèn bằng \(2,8\;\,{\rm{m}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.