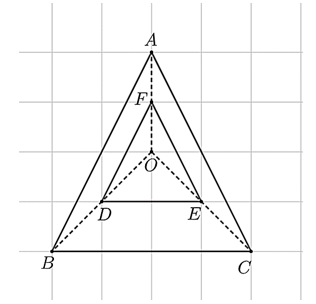
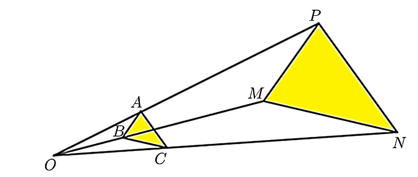
Cho \(\Delta PMN\) là hình đồng dạng phối cảnh của \(\Delta ABC\) với tâm \(O\) và tỉ số vị tự là 3 (hình vẽ).
Quảng cáo
Trả lời:
a) Đúng.
Vì \(\Delta PMN\) là hình đồng dạng phối cảnh của \(\Delta ABC\) với tâm \(O\) và tỉ số vị tự là 3 nên ta có:
\(\frac{{MP}}{{AB}} = \frac{{NP}}{{AC}} = \frac{{MN}}{{BC}} = 3.\)
b) Sai.
\(\Delta MNP\) và \(\Delta ABC\) có: \(\frac{{MP}}{{AB}} = \frac{{NP}}{{AC}} = \frac{{MN}}{{BC}} = 3\) nên (c.c.c). Suy ra: \(\widehat {ABC} = \widehat {NMP}.\)
c) Đúng.
Theo tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{MP}}{{AB}} = \frac{{NP}}{{AC}} = \frac{{MN}}{{BC}} = \frac{{MN + NP + MP}}{{AB + BC + AC}} = 3.\)
Do đó, chu vi tam giác \(MNP\) gấp 3 lần chu vi tam giác \(ABC.\)
d) Sai.
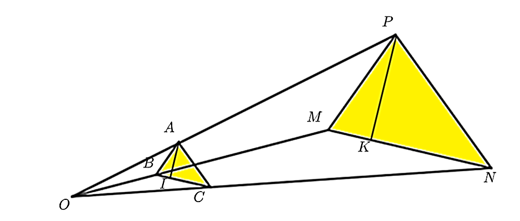
Gọi \(AI,\;\,PK\) lần lượt là đường cao trong các tam giác \(ABC\) và tam giác \(MNP.\)
\(\Delta PKM\) và \(\Delta AIB\) có: \(\widehat {AIB} = \widehat {PKM} = 90^\circ ,\;\,\widehat {ABI} = \widehat {PMK}.\) Do đó, (g.g).
Do đó, \(\frac{{PK}}{{AI}} = \frac{{MP}}{{AB}} = 3.\)
Diện tích tam giác \(ABC\) là: \({S_{ABC}} = \frac{1}{2}AI \cdot BC.\)
Diện tích tam giác \(MNP\) là: \({S_{MNP}} = \frac{1}{2}KP \cdot MN.\)
Ta có: \(\frac{{{S_{MNP}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}KP \cdot MN}}{{\frac{1}{2}AI \cdot BC}} = \frac{{KP}}{{AI}} \cdot \frac{{MN}}{{BC}} = 3 \cdot 3 = 9.\)
Vậy diện tích tam giác \(MNP\) gấp 9 lần diện tích tam giác \(ABC.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(3\)
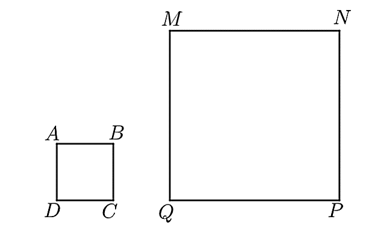
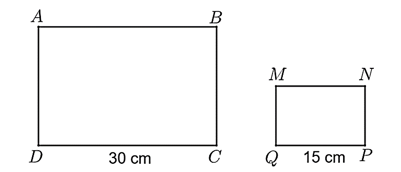
Độ dài cạnh của hình vuông \(ABCD\) là: \(\sqrt {36} = 6\;\,\left( {{\rm{cm}}} \right).\)
Độ dài cạnh của hình vuông \(MNPQ\) là: \(72:4 = 18\;\,\left( {{\rm{cm}}} \right).\)
Hình vuông \(MNPQ\) đồng dạng với hình vuông \(ABCD\) theo tỉ số là: \(18:6 = 3.\)
Vậy hình vuông \(MNPQ\) đồng dạng với hình vuông \(ABCD\) theo tỉ số bằng 3.
Câu 2
Lời giải
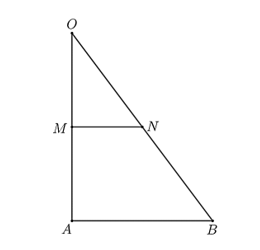
a) Đúng.
Áp dụng định lý Pythagore vào \(\Delta OAB\) vuông tại \(A\) ta có:
\(O{B^2} = O{A^2} + A{B^2} = {8^2} + {6^2} = 100,\) suy ra \(OB = 10\;\,{\rm{cm}}{\rm{.}}\)
Vậy \(OB = 10\;\,{\rm{cm}}{\rm{.}}\)
b) Đúng.
Vì đoạn thẳng \(MN\) là hình đồng dạng phối cảnh của đoạn thẳng \(AB\) tâm \(O\) tỉ số \(0,5\) nên
\(\frac{{MN}}{{AB}} = \frac{{MO}}{{OA}} = \frac{{ON}}{{OB}} = 0,5.\)
c) Đúng.
Vì \(\frac{{MN}}{{AB}} = \frac{{MO}}{{OA}} = \frac{{ON}}{{OB}} = 0,5\) nên
\(MN = 0,5 \cdot AB = 3\;\,\left( {{\rm{cm}}} \right),\;\,MO = 0,5 \cdot OA = 4\;\,\left( {{\rm{cm}}} \right),\;\,ON = 0,5 \cdot OB = 5\;\,\left( {{\rm{cm}}} \right).\)
Chu vi tam giác \(OMN\) là: \(OM + ON + MN = 4 + 5 + 3 = 12\;\,\left( {{\rm{cm}}} \right).\)
Vậy chu vi tam giác \(OMN\) lớn hơn \(10\;\,{\rm{cm}}{\rm{.}}\)
d) Sai.
\(\Delta AOB\) có: \(\frac{{MO}}{{OA}} = \frac{{ON}}{{OB}}\) nên \(MN\;{\rm{//}}\;AB\) suy ra tứ giác \(AMNB\) là hình thang.
Lại có: \(\widehat A = 90^\circ \) nên tứ giác \(AMNB\) là hình thang vuông.
Diện tích hình thang \(AMNB\) là: \(\frac{1}{2}\left( {MN + AB} \right) \cdot MA = \frac{1}{2}\left( {3 + 6} \right) \cdot 4 = 18\;\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Vậy diện tích tứ giác \(AMNB\) nhỏ hơn \(20\;\,{\rm{c}}{{\rm{m}}^2}.\)
Câu 3
b) Hình chữ nhật \(ABCD\) đồng dạng với hình chữ nhật \(MNPQ\) theo tỉ số đồng dạng là 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.