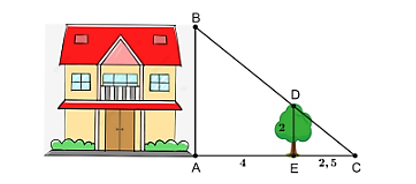
Để đo chiều cao \(AB\) của tòa nhà, người ta đặt một cọc \(CD\) thẳng đứng gần tòa nhà. Trên đầu \(C\) của cọc có gắn một thước ngắm sao cho hướng của thước đi qua đỉnh \(A\) của tòa nhà. Sau đó xác định điểm \(E\) là giao điểm của hai đường thẳng \(AC,\,BD.\) Người ta đo được \(CD = 3\,\,{\rm{m, }}ED = 4\,\,{\rm{m,}}\)\(EB = 72\,\,{\rm{m}}\) (như hình vẽ dưới đây):
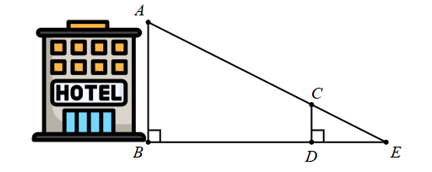
Khi đó,
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đúng.
Áp dụng định lí Pythagore vào tam giác \(EDC\) vuông tại \(D\), có:
\(E{C^2} = D{C^2} + D{E^2}\,\)(định lí Pythagore)
\(E{C^2} = {3^2} + {4^2}\,\)
\(EC = \sqrt {{3^2} + {4^2}\,} = 5\,\,\left( {\rm{m}} \right)\)
b) Sai.
Có \(EB \bot DC,\,\,EB \bot AB\) nên \(CD\parallel AB\).
Do đó, xét tam giác \(EAB\) có: \(\frac{{ED}}{{EB}} = \frac{{EC}}{{EA}}\) (hệ quả của định lí Thalès).
c) Đúng.
Có \(\frac{{ED}}{{EB}} = \frac{{EC}}{{EA}}\) hay \(\frac{4}{{72}} = \frac{5}{{EA}}\) nên \(AE = \frac{{72 \cdot 5}}{4} = 90\,\,\left( {\rm{m}} \right)\).
d) Đúng.
Xét tam giác \(AEB\) vuông tại \(D\) có: \(A{E^2} = A{B^2} + B{E^2}\) (định lí Pythagore)
Do đó, \(AB = \sqrt {{{90}^2} - {{72}^2}} = 54\,\,\left( {\rm{m}} \right)\).
Vậy chiều cao \(AB\) của tòa nhà là 54 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: B
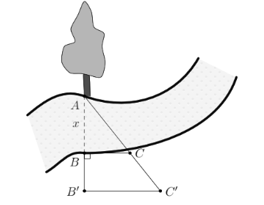
Có \(BC \bot AB',\,B'C' \bot AB'\) nên \(BC\parallel B'C'\).
Do đó, \(\frac{{AB}}{{AB'}} = \frac{{BC}}{{B'C'}}\) (Hệ quả của định lí Thalès)
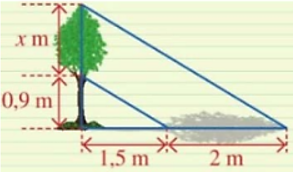
Suy ra \(\frac{{AB}}{{AB + BB'}} = \frac{{BC}}{{B'C'}}\) hay \(\frac{x}{{x + 20}} = \frac{{30}}{{40}}\)
Suy ra \(40x = 30\left( {x + 20} \right)\) nên \(x = 60\,\,\left( {\rm{m}} \right)\).
Câu 2
c) \(\frac{{AB}}{{AD}} = \frac{{ED}}{{CB}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Đúng.
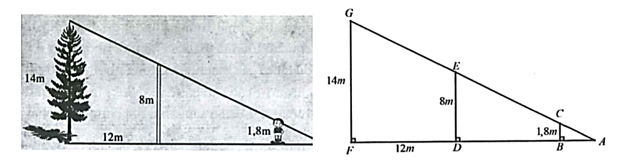
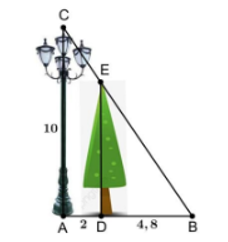
Vì \(CB \bot AF,\,\,ED \bot AF,\,\,GF \bot \,AF\) nên \(CB\parallel ED\parallel GF\).
b) Đúng.
Xét \(\Delta AFG\) có \(ED\parallel GF\) nên \(\frac{{AD}}{{AF}} = \frac{{ED}}{{GF}}\) (hệ quả của định lí Thales)
Suy ra \(\frac{{AD}}{{12}} = \frac{8}{6}\) suy ra \(AD = \frac{{12 \cdot 8}}{6} = 16\,\,\left( {\rm{m}} \right)\,\).
c) Sai.
Xét \(\Delta ADE\) có \(CB\parallel ED\) nên: \(\frac{{AB}}{{AD}} = \frac{{CB}}{{ED}}\) (hệ quả của định lí Thalès)
d) Đúng.
Vì \(\frac{{AB}}{{AD}} = \frac{{CB}}{{ED}}\) nên \(\frac{{AB}}{{16}} = \frac{{1,8}}{8}\) suy ra \(AB = 3,6\,\,\left( {\rm{m}} \right)\).
Do đó, \(BD = AD - AB = 16 - 3,6 = 12,4\,\,\left( {\rm{m}} \right)\).
Vậy người quan sát có chiều cao \(1,8\,\,{\rm{m}}\) phải đứng cách bức tường \(12,4\,\,{\rm{m}}\) để có thể nhìn thấy ngọn.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập