(1 điểm) Một người đi dọc bờ biển từ vị trí \(A\) đến vị trí \(B\) và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ vị trí \(A,\,\,B\) tới ngọn hải đăng với đường đi của người quan sát là \(50^\circ \) và \(70^\circ \). Biết khoảng cách giữa hai vị trí \(A\) và \(B\) là 20 m. Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
(1 điểm) Một người đi dọc bờ biển từ vị trí \(A\) đến vị trí \(B\) và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ vị trí \(A,\,\,B\) tới ngọn hải đăng với đường đi của người quan sát là \(50^\circ \) và \(70^\circ \). Biết khoảng cách giữa hai vị trí \(A\) và \(B\) là 20 m. Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 10 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \(C\) là vị trí ngọn hải đăng, từ \(C\) kẻ \(CH\) vuông góc với đường thẳng \(AB\) tại \(H\). Khi đó \(CH\) là khoảng cách từ ngọn hải đăng tới bờ biển. Ta mô phỏng bài toán như hình vẽ sau:
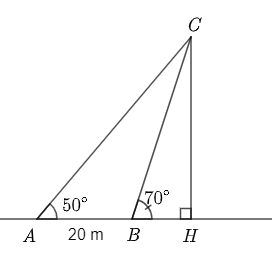
Vì \(\widehat {CBH}\) là góc ngoài tại đỉnh \(B\) của tam giác \(ABC\) nên \(\widehat {CBH} = \widehat {CAB} + \widehat {ACB}\).
Suy ra \(\widehat {ACB} = \widehat {CBH} - \widehat {CAB} = 70^\circ - 50^\circ = 20^\circ \).
Áp dụng định lí sin trong tam giác \(ABC\) ta có:
\(\frac{{AB}}{{\sin \widehat {ACB}}} = \frac{{BC}}{{\sin \widehat {CAB}}}\)\( \Rightarrow BC = \frac{{AB\sin \widehat {CAB}}}{{\sin \widehat {ACB}}} = \frac{{20 \cdot \sin 50^\circ }}{{\sin 20^\circ }} \approx 44,8\).
Tam giác \(CBH\) vuông tại \(H\) nên ta có:
\(CH = BC\sin \widehat {CBH} = 44,8 \cdot \sin 70^\circ \approx 42,1\).
Vậy ngọn hải đăng cách bờ biển khoảng 42,1 m.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
Ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \), suy ra \(\cos A = - \cos \left( {B + C} \right) = - \left( { - \frac{{\sqrt 2 }}{2}} \right) = \frac{{\sqrt 2 }}{2}\) (hai góc bù nhau).
Theo định lí côsin trong tam giác \(ABC\), ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos A = {2^2} + {\left( {2\sqrt 2 } \right)^2} - 2 \cdot 2 \cdot 2\sqrt 2 .\frac{{\sqrt 2 }}{2} = 4\).
Suy ra \(BC = 2\).
Lời giải
Ta phân tích được: \[\overrightarrow {AL} = \frac{b}{{b + c}}\overrightarrow {AB} + \frac{c}{{b + c}}\overrightarrow {AC} \]
\[\overrightarrow {CM} = \frac{{\overrightarrow {CA} + \overrightarrow {CB} }}{2} = \frac{{\overrightarrow {AB} - 2\overrightarrow {AC} }}{2}\]
Theo giả thiết: \[AL \bot CM \Leftrightarrow \overrightarrow {AL} .\overrightarrow {CM} = 0\]
\[ \Leftrightarrow \left( {b\overrightarrow {AB} + c\overrightarrow {AC} } \right)\left( {\overrightarrow {AB} - 2\overrightarrow {AC} } \right) = 0\]
\[ \Leftrightarrow b{c^2} + b{c^2}\cos A - 2c{b^2}\cos A - 2c{b^2} = 0\]
\[ \Leftrightarrow \left( {c - 2b} \right)\left( {1 + \cos A} \right) = 0 \Rightarrow c = 2b\,\,\left( {do\,\,\cos A > - 1} \right)\]
Khi đó: \[C{M^2} = \frac{{{b^2} + {a^2}}}{2} - \frac{{{c^2}}}{4} = \frac{{{a^2} - {b^2}}}{2}\]
\[A{L^2} = \frac{1}{9}{\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)^2} = \frac{1}{9}\left( {A{B^2} + A{C^2} + 2\overrightarrow {AB} \cdot \overrightarrow {AC} } \right) = \frac{2}{9}\left( {9{b^2} - {a^2}} \right)\]
\[\frac{{CM}}{{AL}} = \frac{{\sqrt 3 }}{2} \Leftrightarrow \frac{{C{M^2}}}{{A{L^2}}} = \frac{9}{4}.\frac{{{a^2} - {b^2}}}{{9{b^2} - {a^2}}} = \frac{3}{4} \Leftrightarrow {a^2} = 3{b^2}\]
Do đó, \[\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{b^2} + {{\left( {2b} \right)}^2} - 3{b^2}}}{{2b \cdot 2b}} = \frac{1}{2}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập