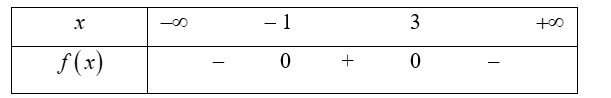Tam giác \(ABC\) có \(AB = 3\,cm\), \(BC = 4\,cm\), \(\widehat {ABC} = 60^\circ \). Độ dài cạnh \(AC\) bằng
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 10 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
Xét tam giác \(ABC\)
Áp dụng định lí côsin ta có:
\(A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos \widehat {ABC}\)
Thay số \(AB = 3\,cm\), \(BC = 4\,cm\), \(\widehat {ABC} = 60^\circ \) ta có:
\(A{C^2} = {3^2} + {4^2} - 2.3.4.\cos 60^\circ = 13\)
Do \(AC\) > 0 nên \(AC = \sqrt {13} \)cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lợi nhuận của công ty trong một tháng khi bán hết \(q\) sản phẩm là:
\(L\left( q \right) = q.R\left( q \right) - C\left( q \right) = q\left( {120 - 2q} \right) - \left( {4{q^2} + 36q - 1\,\,234} \right)\)\( = - 6{q^2} + 84q + 1\,234\).
Để lợi nhuận công ty thu về là cao nhất, tức cần tìm \(q\) để \(L\left( q \right)\) đạt giá trị lớn nhất.
Lại có \(L\left( q \right) = - 6{q^2} + 84q + 1\,234\) là hàm số bậc hai có hệ số \(a = - 6 < 0\), nên nó đạt giá trị lớn nhất tại đỉnh.
Ta có: \(q = - \frac{b}{{2a}} = - \frac{{84}}{{2.\left( { - 6} \right)}} = 7\). Do đó, \(L\left( q \right)\)đạt giá trị lớn nhất tại \(q = 7\).
Vậy công ty A cần sản xuất 7 sản phẩm trong một tháng để thu về lợi nhuận cao nhất.
Lời giải
Đáp án đúng là: C
\(\sqrt { - {x^2} + 4x - 3} = \sqrt {2m + 3x - {x^2}} \)\( \Leftrightarrow \left\{ \begin{array}{l} - {x^2} + 4x - 3 \ge 0\\ - {x^2} + 4x - 3 = 2m + 3x - {x^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}1 \le x \le 3\\x = 2m + 3\end{array} \right.\)
Để phương trình (1) có nghiệm thì \(1 \le 2m + 3 \le 3 \Leftrightarrow - 1 \le m \le 0 \Rightarrow m \in \left[ { - 1;\,\,0} \right]\).
Suy ra \(a = - 1,\,\,b = 0\), do đó \({a^2} + {b^2} = {\left( { - 1} \right)^2} + {0^2} = 1\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.