(1 điểm) Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với tốc độ 540 km/h theo hướng đông và chiếc còn lại di chuyển theo hướng \({\rm{N25^\circ E}}\)với tốc độ 670 km/h. Hỏi sau 2 tiếng, hai máy bay cách nhau bao xa? Giả sử chúng đang ở cùng độ cao.
(1 điểm) Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với tốc độ 540 km/h theo hướng đông và chiếc còn lại di chuyển theo hướng \({\rm{N25^\circ E}}\)với tốc độ 670 km/h. Hỏi sau 2 tiếng, hai máy bay cách nhau bao xa? Giả sử chúng đang ở cùng độ cao.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 10 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Gọi \(O,\,\,A,\,\,B\) lần lượt là vị trí sân bay và hai máy bay sau 2 tiếng.
Hướng \({\rm{N25^\circ E}}\) là hướng tạo với hướng bắc một góc \(25^\circ \) và tạo với hướng đông một góc \(90^\circ - 25^\circ = 65^\circ \). Ta mô phỏng bài toán đã cho như sau:
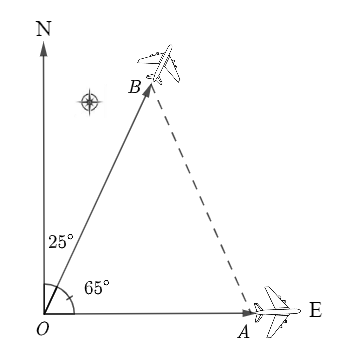
Quãng đường máy bay bay theo hướng đông sau 2 tiếng là
\(OA = 540 \cdot 2 = 1\,\,080\) (km).
Quãng đường máy bay bay theo hướng \({\rm{N25^\circ E}}\) sau 2 tiếng là
\(OB = 670 \cdot 2 = 1\,\,340\) (km).
Ta có: \(\widehat {AOB} = 65^\circ \), \(OA = 1\,\,080,\,\,OB = 1\,\,340\).
Áp dụng định lí côsin trong tam giác \(OAB\), ta có:
\(A{B^2} = O{A^2} + O{B^2} - 2 \cdot OA \cdot OB \cdot \cos \widehat {AOB}\)
\( = 1\,\,{080^2} + 1\,\,{340^2} - 2 \cdot 1\,\,080 \cdot \,1\,\,340 \cdot \cos 65^\circ \approx 1\,\,738\,\,774\).
Suy ra \(AB \approx \sqrt {1\,\,738\,\,774} \approx 1\,\,319\) (km).
Vậy sau 2 tiếng, hai máy bay cách nhau khoảng 1 319 km.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: A
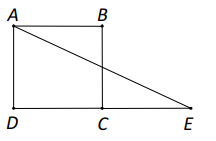
Vì \(E\) là điểm đối xứng của \(D\) qua \(C\) nên \(C\) là trung điểm của \(DE\), do đó \(DE = 2DC = 2 \cdot 3 = 6\).
Ta có: \(\overrightarrow {AE} \cdot \overrightarrow {AB} = \left( {\overrightarrow {AD} + \overrightarrow {DE} } \right) \cdot \overrightarrow {AB} = \overrightarrow {AD} \cdot \overrightarrow {AB} + \overrightarrow {DE} \cdot \overrightarrow {AB} \)
Do \(AB \bot AD\) nên \(\overrightarrow {AD} \cdot \overrightarrow {AB} = 0\).
Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DE} \) cùng hướng nên \(\cos \left( {\overrightarrow {AB} ,\,\,\overrightarrow {DE} } \right) = 0^\circ \).
Do đó,
Vậy \(\overrightarrow {AE} \cdot \overrightarrow {AB} = 0 + 18 = 18\).
Lời giải
Đáp án đúng là: B
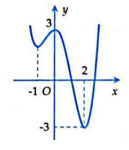
Từ hình vẽ ta thấy, đồ thị hàm số \(y = f\left( x \right)\) đi lên từ trái qua phải trên khoảng \(\left( { - 1;\,\,0} \right)\), do đó hàm số này đồng biến trên khoảng \(\left( { - 1;\,\,0} \right)\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.