(1 điểm) Cho tam giác \(ABC\), điểm \(L\) là trung điểm của \(BC\). Gọi \(M\), \(N\), \(P\) lần lượt là các điểm thỏa mãn các đẳng thức \(\overrightarrow {AM} = a\overrightarrow {AB} \), \(\overrightarrow {AN} = b\overrightarrow {AL} \), \(\overrightarrow {AP} = c\overrightarrow {AC} \). Biết \(abc \ne 0\). Tìm đẳng thức điều kiện của \(a\), \(b\), \(c\) để \(M\), \(N\), \(P\) thẳng hàng.
(1 điểm) Cho tam giác \(ABC\), điểm \(L\) là trung điểm của \(BC\). Gọi \(M\), \(N\), \(P\) lần lượt là các điểm thỏa mãn các đẳng thức \(\overrightarrow {AM} = a\overrightarrow {AB} \), \(\overrightarrow {AN} = b\overrightarrow {AL} \), \(\overrightarrow {AP} = c\overrightarrow {AC} \). Biết \(abc \ne 0\). Tìm đẳng thức điều kiện của \(a\), \(b\), \(c\) để \(M\), \(N\), \(P\) thẳng hàng.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 10 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Ta có:
\(\overrightarrow {MP} = \overrightarrow {AP} - \overrightarrow {AM} = c\overrightarrow {AC} - a\overrightarrow {AB} \)
\(\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = b\overrightarrow {AL} - a\overrightarrow {AB} \)
Mà \(\overrightarrow {AL} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\) (do điểm \(L\) là trung điểm của \(BC\)).
Do đó, ta có: \(\overrightarrow {MN} = \frac{b}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) - a\overrightarrow {AB} = \left( {\frac{b}{2} - a} \right)\overrightarrow {AB} + \frac{b}{2}\overrightarrow {AC} \)
Do \(abc \ne 0\) nên \(M\), \(N\), \(P\) thẳng hàng khi và chỉ khi \(\frac{{\frac{b}{2} - a}}{{ - a}} = \frac{{\frac{b}{2}}}{c} \Leftrightarrow 2ac = ab + bc\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) (nghìn đồng) là số tiền tăng thêm khi bán ra một cốc trà sữa \(\left( {x \ge 0} \right)\).
Số cốc trà sữa bán được sau khi tăng giá thêm \(x\) (nghìn đồng) là: \(2\,200 - 100x\) (cốc).
Số tiền lãi thu được là:
\(\left( {30 + x - 22} \right)\left( {2\,\,200 - 100x} \right) = \left( {8 + x} \right)\left( {2\,200 - 100x} \right) = - 100{x^2} + 1\,400x + 17600\) (nghìn đồng).
Để lợi nhuận thu được là lớn nhất thì phải tìm được \(x\) sao cho hàm số \(f\left( x \right) = - 100{x^2} + 1400x + 17600\) lớn nhất.
Hàm số này là hàm số bậc hai có \(a = - 100 < 0\) nên nó đạt giá trị lớn nhất tại đỉnh của đồ thị hàm số.
Hoành độ đỉnh của đồ thị hàm số \(f\left( x \right) = - 100{x^2} + 1400x + 17600\) là \(x = - \frac{b}{{2a}} = - \frac{{1400}}{{2.\left( { - 100} \right)}} = 7\) (thỏa mãn \[x \ge 0\]).
Khi đó số tiền phải tăng lên để lợi nhuận lớn nhất là 7 nghìn đồng hay chính là bán ra một cốc trà sữa với giá 30 + 7 = 37 (nghìn đồng).
Vậy cửa hàng phải bán mỗi cốc trà sữa với giá 37 000 đồng để đạt lợi nhuận lớn nhất.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ sau:
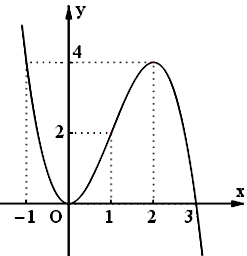
Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.