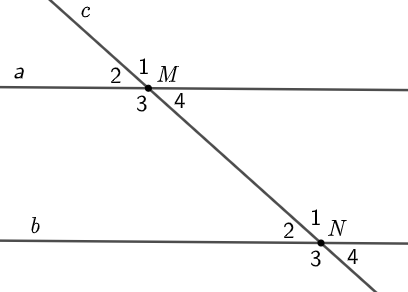
Cho \[a\parallel b\], \(c\) cắt \(a\) và \(b\) lần lượt tại hai điểm \(M\) và \(N\) (như hình vẽ). Khi đó, \[{\widehat M_1}\] bằng số đo góc nào dưới đây?

Biết \[{\widehat M_1} \ne 90^\circ \].

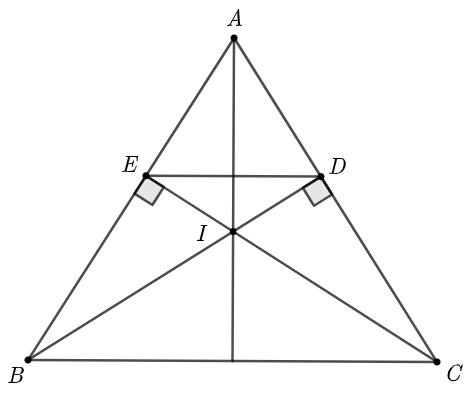
a) Xét \(\Delta ABD\) và \(\Delta ACE\) có:

\(\widehat {ADB} = \widehat {AEC} = 90^\circ \);

\(\widehat {BAC}\) chung;

\(AB = AC\) (\(\Delta ABC\) cân tại \(A\)).

Do đó \(\Delta ABD = \Delta ACE\) (cạnh huyền – góc nhọn).

Suy ra \(AD = AE\) (hai cạnh tương ứng)

Do đó tam giác \(ADE\) cân tại \(A\).

b) \(\Delta ABC\) cân tại \(A\) nên \(\widehat {ACB} = \frac{{180^\circ - \widehat {BAC}}}{2}\)   \(\left( 1 \right)\)

\(\Delta ADE\) cân tại \(A\) nên \(\widehat {ADE} = \frac{{180^\circ - \widehat {BAC}}}{2}\)   \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {ADE} = \widehat {ACB}\).

Mà \(\widehat {ADE}\) và \(\widehat {ACB}\) ở vị trí đồng vị.

Do đó \[DE\parallel BC\].

c) Ta có: \(\widehat {ABC} = \widehat {ABI} + \widehat {IBC}\); \(\widehat {ACB} = \widehat {ACI} + \widehat {ICB}\).

Mà \(\widehat {ABC} = \widehat {ACB}\) (\(\Delta ABC\) cân tại \(A\)); \(\widehat {ABI} = \widehat {ACI}\) (vì \[\Delta ABD = \Delta ACE\]).

Nên \[\widehat {IBC} = \widehat {ICB}\] suy ra \(\Delta IBC\) cân tại \(I\).

Do đó \(IB = IC\).

d) Ta có \(AB = AC\) (\(\Delta ABC\) cân tại \(A\)).

Suy ra điểm \(A\) nằm trên đường trung trực của đoạn thẳng \(BC\).

Mặt khác \(I\) nằm trên đường trung trực của đoạn thẳng \(BC\).

Khi đó \(AI\) là đường trung trực của đoạn thẳng \(BC\).

Do đó \(AI \bot BC\).

Tổng số tiền cần để mua bánh khi chưa giảm giá là:

\(2\,\,.\,11,5 + 3\,\,.\,9,5 + 2\,\,.\,6,75 = 65\) (đô la)

Số tiền bạn Peter cần để mua bánh khi đã giảm giá là:

\(65 - 65\,\,.\,\,10\% = 58,5\) (đô la)

Số tiền người bán hàng phải trả lại cho Peter là:

\(100 - 58,5 = 41,5\) (đô la).

Vậy người bán hàng phải trả lại cho Peter là 41,5 đô la.