PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.

Trong các số sau, phân số nào biểu diễn số hữu tỉ \(\frac{{ - 4}}{5}\)?

Sau đợt thứ nhất, bác Minh lãi số tiền là:

\(30\,\,.\,\,\left( {9,8 - 8} \right) = 54\) (triệu đồng).

Sau đợt thứ hai, bác Minh lãi số tiền là:

\(10\,\,.\,\,\left( {9,5 - 8} \right) = 15\) (triệu đồng).

Để lợi nhuận đạt tỉ lệ 20% thì số tiền lãi bác Minh thu được là:

\(50\,\,.\,\,8\,\,.\,\,20\% = 80\) (triệu đồng).

Số chiếc điện thoại còn lại sau hai đợt bán là:

\(50 - 30 - 10 = 10\) (chiếc điện thoại).

Số tiền lãi cần đạt được khi bán 10 chiếc điện thoại còn lại là:

\[80 - 54 - 15 = 11\] (triệu đồng).

Với 10 chiếc điện thoại có giá 11 triệu đồng thì giá tiền mỗi chiếc điện thoại là:

\(11\,\,:\,\,10 = 1,1\) (triệu đồng).

Vậy bác Minh phải bán mỗi chiếc điện thoại còn lại với giá 1,1 triệu đồng để lợi nhuận đạt tỉ lệ 20%.

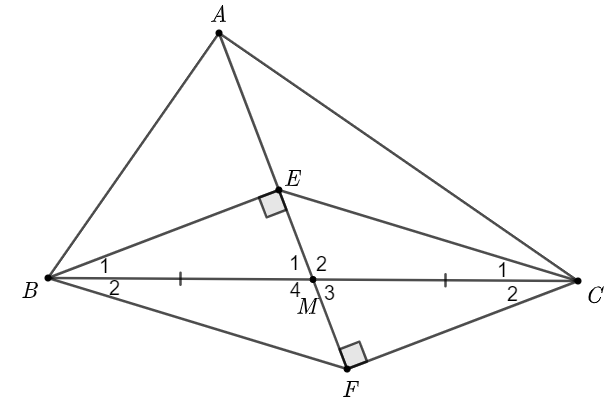
a) Theo giả thiết: \(BE \bot Ax\), \(CF \bot Ax\)

Suy ra \(BE\parallel CF\).

b) So sánh \(BE\) và \(FC\); \(CE\) và \(BF\).

• Xét \(\Delta MBE\) và \(\Delta MCF\) có:

\({\widehat B_1} = {\widehat C_2}\) (hai góc so le trong);

\(BM = CM\) (vì \(M\) là trung điểm của \(BC\));

\({\widehat M_1} = {\widehat M_3}\) (hai góc đối đỉnh).

Do đó \(\Delta MBE = \Delta MCF\) (g.c.g)

Suy ra \(BE = CF\) (hai cạnh tương ứng).

• Xét \(\Delta MBF\) và \(\Delta MCE\) có:

\({\widehat B_2} = {\widehat C_1}\) (hai góc so le trong);

\(BM = CM\) (vì \(M\) là trung điểm của \(BC\));

\({\widehat M_2} = {\widehat M_4}\) (hai góc đối đỉnh).

Do đó \(\Delta MBF = \Delta MCE\) (g.c.g)

Suy ra \(BF = CE\) (hai cạnh tương ứng).

Vậy \(BE = CF\); \(BF = CE\).

c) Xét \(\Delta BEM\) và \(\Delta CEM\) có:

\(BE = CE\) (giả thiết);

\(BM = CM\) (vì \(M\) là trung điểm của \(BC\));

\(EM\) là cạnh chung

Do đó \(\Delta BEM = \Delta CEM\) (c.c.c).

d) Từ câu c: \(\Delta BEM = \Delta CEM\)

Suy ra \(\widehat {BME} = \widehat {CME}\) (hai góc tương ứng).

Mặt khác, \(\widehat {BME} + \widehat {CME} = 180^\circ \) (hai góc kề bù) nên \(\widehat {BME} = \widehat {CME} = 90^\circ \).

Suy ra \(EM \bot BC\) hay \(AM \bot BC\).

Xét \(\Delta BAM\) và \(\Delta CAM\) có:

\(BM = CM\) (vì \(M\) là trung điểm của \(BC\));

\(\widehat {BAM} = \widehat {CAM} = 90^\circ \);

\(AM\) là cạnh chung

Do đó \(\Delta BAM = \Delta CAM\) (c.g.c).

Suy ra \(AB = AC\) (hai cạnh tương ứng).

Do đó tam giác \(ABC\) cân tại \(A\).

Vậy tam giác \(ABC\) cân tại \(A\) thì \(BE = CE\).