Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: D
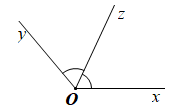
Phương án A sai vì hai góc có tổng bằng \(180^\circ \) nhưng không kề nhau thì không phải là hai góc kề bù.
Phương án B sai, chẳng hạn \(\widehat {xOz} = \widehat {zOy}\) và có chung đỉnh \(O\) nhưng không phải hai góc đối đỉnh.
Phương án C sai vì qua một điểm nằm ngoài một đường thẳng thì chỉ có duy nhất 1 đường thẳng song song với đường thẳng đó.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x,y,z\) lần lượt là số trang mà người thứ nhất, người thứ hai, người thứ ba đánh máy được.
Cả ba người cùng đánh máy cuốn sách có 555 trang nên \(x + y + z = 555\).
Vì cả ba người cùng làm từ lúc đầu cho đến khi xong nên thời gian ba người cùng làm là như nhau, vì vậy số trang và thời gian đánh mỗi trang là hai đại lượng tỉ lệ nghịch với nhau.
Do đó ta có \(5x = 4y = 6z\) suy ra \(\frac{{5x}}{{60}} = \frac{{4y}}{{60}} = \frac{{6z}}{{60}}\) hay \(\frac{x}{{12}} = \frac{y}{{15}} = \frac{z}{{10}}\).
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{{12}} = \frac{y}{{15}} = \frac{z}{{10}} = \frac{{x + y + z}}{{12 + 15 + 10}} = \frac{{555}}{{37}} = 15\)
Suy ra \(x = 12.15 = 180\); \(y = 15.15 = 225\); \(z = 10.15 = 150\).
Vậy người thứ nhất, người thứ hai, người thứ ba đánh được lần lượt 180 trang; 225 trang; 150 trang.
Lời giải
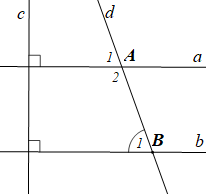
a) Học sinh vẽ lại hình theo đúng số đo các góc.
|
GT |
\(a,b,c,d\) là các đường thẳng; \(c \bot a\); \(c \bot b\); \(d\) cắt \(a\) tại \(A\); \(d\) cắt \(b\) tại \(B\). b) \({\widehat A_1} = \frac{7}{{11}}\widehat {{A_2}}\). |
|
KL |
b) Giải thích \(a\,{\rm{//}}\,b\). c) Tính \({\widehat B_2}\). |
b) Vì \(c \bot a\); \(c \bot b\) nên \(a\,{\rm{//}}\,b\) (hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau).
c) Ta có \({\widehat A_1} + {\widehat A_2} = 180^\circ \) (hai góc kề bù)
Mà \({\widehat A_1} = \frac{7}{{11}}\widehat {{A_2}}\) nên \(\frac{7}{{11}}{\widehat A_2} + {\widehat A_2} = 180^\circ \), hay \(\frac{{18}}{{11}}{\widehat A_2} = 180^\circ \)
Suy ra \({\widehat A_2} = 110^\circ \).
Do \(a\,{\rm{//}}\,b\) (câu b) nên \({\widehat A_2} + {\widehat B_1} = 180^\circ \) (hai góc trong cùng phía)
Do đó \({\widehat B_1} = 180^\circ - {\widehat A_2} = 180^\circ - 110^\circ = 70^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(y = - 2x\);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.