Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Gọi \(x,y,z\) lần lượt là số máy in của các phân xưởng thứ nhất, thứ hai, thứ ba.
Tổng số máy của ba phân xưởng là \(x + y + z = 57\).
Vì số ngày hoàn thành công việc tỉ lệ nghịch với số máy in nên ta có:
\(2x = 4y = 5z\) suy ra \(\frac{{2x}}{{20}} = \frac{{4y}}{{20}} = \frac{{5z}}{{20}}\) hay \(\frac{x}{{10}} = \frac{y}{5} = \frac{z}{4}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{10}} = \frac{y}{5} = \frac{z}{4} = \frac{{x + y + z}}{{10 + 5 + 4}} = \frac{{57}}{{19}} = 3\)
Suy ra \(x = 3.10 = 30\); \(y = 3.5 = 15\); \(z = 3.4 = 12\).
Vậy số máy in của ba phân xưởng lần lượt là \(30;15;12\) (máy in).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Từ \(\frac{{a + b}}{{c + d}} = \frac{{b + c}}{{d + a}}\) suy ra \(\frac{{a + b}}{{b + c}} = \frac{{c + d}}{{d + a}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\[\frac{{a + b}}{{b + c}} = \frac{{c + d}}{{d + a}} = \frac{{a + b + c + d}}{{b + c + d + a}} = 1\]
Do đó \(a + b = b + c\) nên \(a = c\).
Câu 2
Lời giải
Đáp án đúng là: C
Ta có \(\frac{{ - 3}}{{15}} = \frac{{ - 1}}{5}\). Phân số \(\frac{{ - 1}}{5}\) và \(\frac{{ - 1}}{{20}}\) là các phân số tối giản với mẫu số dương có ước nguyên tố là 2 và 5 nên viết được dưới dạng số thập phân hữu hạn.
Số \(\sqrt 3 \) là căn bậc hai số học của số 3, số 3 không phải số chính phương nên \(\sqrt 3 \) là số vô tỉ.
Số \(\frac{4}{{ - 12}} = \frac{{ - 1}}{3}\) là phân số tối giản với mẫu số dương có ước nguyên tố khác là 2 và 5 nên viết được dưới dạng số thập phân vô hạn tuần hoàn.
Câu 3
(2,0 điểm) Cho hình vẽ biết \(xx' \bot tt'\), \[yy' \bot tt'\], \(\widehat {zCx'} = 110^\circ \), \(\widehat {CAO} = 50^\circ \), \(\widehat {OBy'} = 140^\circ \).
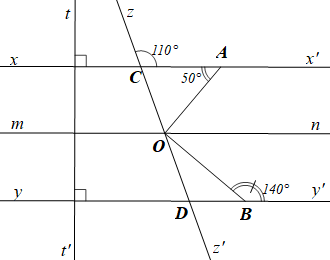
a) Vẽ lại hình (đúng số đo của các góc) và viết giả thiết, kết luận của bài toán.
b) Giải thích tại sao \(xx'\,{\rm{//}}\,yy'\).
c) Tìm số đo của \(\widehat {CDy}\).
d) Tìm số đo của \(\widehat {AOB}\).
(2,0 điểm) Cho hình vẽ biết \(xx' \bot tt'\), \[yy' \bot tt'\], \(\widehat {zCx'} = 110^\circ \), \(\widehat {CAO} = 50^\circ \), \(\widehat {OBy'} = 140^\circ \).

a) Vẽ lại hình (đúng số đo của các góc) và viết giả thiết, kết luận của bài toán.
b) Giải thích tại sao \(xx'\,{\rm{//}}\,yy'\).
c) Tìm số đo của \(\widehat {CDy}\).
d) Tìm số đo của \(\widehat {AOB}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.