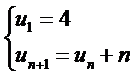Tính tổng \[S\] của các nghiệm của phương trình \[\sin x = \frac{1}{2}\] trên đoạn \[\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\].
A. \[S = \frac{\pi }{2}\].
B. \[S = \frac{\pi }{6}\].
C. \[S = \frac{\pi }{3}\].
D. \[S = \frac{{5\pi }}{6}\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
Ta có: \[\sin x = \frac{1}{2} \Leftrightarrow \sin x = \sin \frac{\pi }{6} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{6} + k2\pi \end{array} \right.,k \in \mathbb{Z}\]
\[x \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right] \Rightarrow x = \frac{\pi }{6}\].
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(14\).
B. \(28\).
C. \(10\).
D. \(8\).
Lời giải
Chọn C
Có \({u_2} = {u_1} + 1 = 5;{u_3} = {u_2} + 2 = 7;{u_4} = {u_3} + 3 = 10\)
Câu 2
A. \[x = \frac{\pi }{6} + k\pi ,\,k \in \mathbb{Z}\].
B. \[x = \frac{\pi }{3} + k\pi ,\,\,k \in \mathbb{Z}\].
C. Vô nghiệm.
D. \[x = \frac{\pi }{6} + k2\pi ,\,k \in \mathbb{Z}\].
Lời giải
Chọn A
\(3\tan \,x - \sqrt 3 = 0 \Leftrightarrow \tan \,x = \frac{{\sqrt 3 }}{3} \Leftrightarrow \tan \,x = \tan \frac{\pi }{6} \Leftrightarrow \)\[x = \frac{\pi }{6} + k\pi ,\,k \in \mathbb{Z}\].
Câu 3
A. \({u_n} = n - 2\).
B. \({u_n} = - {n^2} - 6n\).
C. \({u_n} = 1 - 2n\).
D. \({u_n} = {\left( { - 1} \right)^n}.{n^2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\left( {{w_n}} \right)\) với \({w_n} = \frac{n}{{{2^n}}}\,\,\,\left( {\forall n \in {\mathbb{N}^*}} \right)\).
B. \(\left( {{v_n}} \right)\) với \({v_n} = \frac{n}{{n + 2}}\,\,\left( {\forall n \in {\mathbb{N}^*}} \right)\).
C. \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{n - 1}}{{{2^n}}}\,\,\left( {\forall n \in {\mathbb{N}^*}} \right)\).
D. \(\left( {{t_n}} \right)\) với \({t_n} = \frac{1}{{n + 1}}\,\,\,\left( {\forall n \in {N^*}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\left( { - \pi ;0} \right)\).
B. \(\left( {0;\pi } \right)\).
C. \(\left( {\frac{\pi }{2};\pi } \right)\).
D. \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(x = 64\).
B. \(x = 24\).
C. \(x = 32\).
D. \(x = 16\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \({u_n} = 3 + {3^n}\).
B. \({u_n} = {3^{n - 1}}\).
C. \({u_n} = {3^{n + 1}}\).
D. \({u_n} = {3^n}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập