Một học sinh đứng tại vị trí A trên ban công tầng 3 của trường THPT chuyên Lê Quý Đôn nhìn xuống bên kia đường thấy 2 chiếc xe ô tô đậu ở vị trí B và C. Biết các góc nhìn xuống từ A đến B và C theo phương ngang lần lượt là \(\frac{\pi }{{10}}\) và \(\frac{\pi }{{12}}\) (minh họa như hình vẽ), độ cao từ vị trí A đến mặt đất là \[AH = 10{\rm{m}}\] và các điểm H, B, C thẳng hàng. Tính khoảng cách giữa hai xe ô tô (không được sử dụng máy tính cầm tay để tính xấp xỉ kết quả).
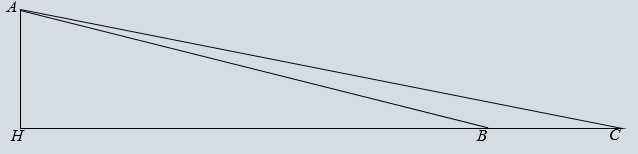
Một học sinh đứng tại vị trí A trên ban công tầng 3 của trường THPT chuyên Lê Quý Đôn nhìn xuống bên kia đường thấy 2 chiếc xe ô tô đậu ở vị trí B và C. Biết các góc nhìn xuống từ A đến B và C theo phương ngang lần lượt là \(\frac{\pi }{{10}}\) và \(\frac{\pi }{{12}}\) (minh họa như hình vẽ), độ cao từ vị trí A đến mặt đất là \[AH = 10{\rm{m}}\] và các điểm H, B, C thẳng hàng. Tính khoảng cách giữa hai xe ô tô (không được sử dụng máy tính cầm tay để tính xấp xỉ kết quả).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Theo đề ta có \(\widehat {HBA} = \frac{\pi }{{10}}\,\,,\,\,\widehat {HCA} = \frac{\pi }{{12}}\)
Khoảng cách giữa hai xe ô tô: \(BC = HC - HB = \frac{{10}}{{\tan \frac{\pi }{{12}}}} - \frac{{10}}{{\tan \frac{\pi }{{10}}}}\)
\(\tan \frac{\pi }{{12}} = \tan \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right) = \frac{{\tan \frac{\pi }{3} - \tan \frac{\pi }{4}}}{{1 + \tan \frac{\pi }{3}.\tan \frac{\pi }{4}}} = \frac{{\sqrt 3 - 1}}{{1 + \sqrt 3 }} = 2 - \sqrt 3 \)Ta có: \(\cos \frac{{2\pi }}{{10}} = \sin \frac{{3\pi }}{{10}}\)
\(\begin{array}{l} \Rightarrow 1 - 2{\sin ^2}\frac{\pi }{{10}} = 3\sin \frac{\pi }{{10}} - 4{\sin ^3}\frac{\pi }{{10}}\\ \Rightarrow \left[ \begin{array}{l}\sin \frac{\pi }{{10}} = 1\,\,\,\,\left( L \right)\\\sin \frac{\pi }{{10}} = \frac{{ - 1 + \sqrt 5 }}{4}\,\,\,\,\left( N \right)\\\sin \frac{\pi }{{10}} = \frac{{ - 1 - \sqrt 5 }}{4}\,\,\,\,\left( L \right)\end{array} \right.\end{array}\)
+ \(\cos \frac{\pi }{{10}} = \sqrt {1 - {{\sin }^2}\frac{\pi }{{10}}} = \frac{{\sqrt {10 + 2\sqrt 5 } }}{4}\)
+ \(\tan \frac{\pi }{{10}} = \frac{{\sin \frac{\pi }{{10}}}}{{\cos \frac{\pi }{{10}}}} = \frac{{\sqrt 5 - 1}}{{\sqrt {10 + 2\sqrt 5 } }}\)
Vậy \(BC = \frac{{10}}{{2 - \sqrt 3 }} - 10\frac{{\sqrt {10 + 2\sqrt 5 } }}{{\sqrt 5 - 1}} = 10\left( {2 + \sqrt 3 } \right) - \frac{5}{2}.\sqrt {10 + 2\sqrt 5 } \left( {\sqrt 5 + 1} \right)\).Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn B
Gọi tiên lương bác Y năm thứ \(n\) là \({u_n} \Rightarrow \left( {{u_n}} \right)\) là một cấp số nhân với \({u_1} = 42\) triệu công công bội \(q = 1,05\)
Tổng số tiền lương bác Y nhận được sau 15 năm là: \({S_{15}} = {u_1}.\frac{{1 - {q^{15}}}}{{1 - q}} = 42.\frac{{1 - 1,{{05}^{15}}}}{{1 - 1,05}} \approx 906,3\)
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn B
Với mọi \(t \in \mathbb{R}\), ta có:
\( - 4 \le 4\sin \left[ {\frac{\pi }{8}\left( {t - 9} \right)} \right] \le 4 \Leftrightarrow 23 \le 4\sin \left[ {\frac{\pi }{8}\left( {t - 9} \right)} \right] + 27 \le 31\)
\( \Rightarrow \mathop {\max }\limits_\mathbb{R} h\left( t \right) = 31\) khi \(\sin \left[ {\frac{\pi }{8}\left( {t - 9} \right)} \right] = 1 \Leftrightarrow t = 13 + 16k,k \in \mathbb{Z}\)
\(t \in \left[ {0;24} \right] \Rightarrow t = 13\)
Vậy nhiệt độ cao nhất trong ngày \(31^\circ {\rm{C}}\), lúc 13 giờ.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập