a) Tìm tập xác định của hàm số \(y = \frac{{\cos x}}{{\sin x + 1}}\)
b) Tìm \(a\) để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,\,x \le 1\\\frac{{{x^3} - {x^2} + 2x - 2}}{{x - 1}}\,\,\,{\rm{khi}}\,\,\,x > 1\,.\end{array} \right.\)liên tục tại \(x = 1\)
Quảng cáo
Trả lời:
a,
Điều kiện \(\sin x + 1\not = 0 \Leftrightarrow \sin x\not = - 1 \Leftrightarrow x\not = - \frac{\pi }{2} + k2\pi \left( {k \in Z} \right)\).
Vậy tập xác định \(D = R{\rm{\backslash }}\left\{ { - \frac{\pi }{2} + k2\pi |k \in Z} \right\}\).
b,
Xét tính liên tục của hàm số tại điểm \(x = 1\), ta có:
+ \[f\left( 1 \right) = 2 + a\].
+ \[\mathop {\lim }\limits_{x\, \to \,{1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x\, \to \,{1^ - }} \left( {2x + a} \right) = 2 + a\].
+ \[\mathop {\lim }\limits_{x\, \to \,{1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x\, \to \,{1^ + }} \frac{{{x^3} - {x^2} + 2x - 2}}{{x - 1}} = \mathop {\lim }\limits_{x\, \to \,{1^ + }} \frac{{\left( {x - 1} \right)\left( {{x^2} + 2} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x\, \to \,{1^ + }} \left( {{x^2} + 2} \right) = 3\].
Hàm số \(f\left( x \right)\) liên tục trên \(R\) \( \Leftrightarrow \) hàm số \(f\left( x \right)\) liên tục tại \(x = 1\)
Û \[\mathop {\lim }\limits_{x\, \to \,{1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x\, \to \,{1^ + }} f\left( x \right) = f\left( 1 \right)\] Û \[2a + 1 = 3\] Û \(a = 1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
|
Thời gian (phút) |
[9,5:12,5) |
[12,5; 15,5) |
\[\left[ {15,5;{\rm{ }}18,5} \right)\] |
[18,5; 21,5) |
[21,5; 24,5) |
|
Số học sinh |
3 |
12 |
15 |
24 |
2 |
Trung vị của mẫu số liệu ghép nhóm này bằng:
Lời giải
Chọn A
\(n = 3 + 12 + 15 + 24 + 2 = 56\)
Gọi \[{x_1},{x_2},...{x_{56}}\] là thời gian (phút) truy cập Internet mỗi buổi tối của 56 học sinh theo thứ tự không giảm.
Khi đó trung vị thuộc \[\left[ {15,5;{\rm{ }}18,5} \right)\]
\[{M_e} = 15,5 + \frac{{\frac{{56}}{2} - \left( {3 + 12} \right)}}{{15}}.\left( {18,5 - 15,5} \right) = 18,1\]
Lời giải
a,
Ta có:
S là điểm chung thứ nhất, O là điểm chung thứ hai
Do đó: \[\left( {SAC} \right) \cap \left( {SBD} \right) = SO\]
b,
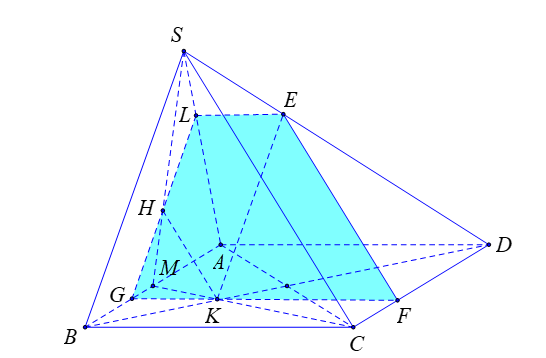
+ Gọi \(M\) là trung điểm của \[AB\].
Vì \(H,\;K\) lần lượt là trọng tâm tam giác \(SAB\) và \(ABC\) nên \(\frac{{MH}}{{MS}} = \frac{{MK}}{{MC}} = \frac{1}{3}\).
\( \Rightarrow HK\;{\rm{//}}\;SC\).
Mà \(SC \subset \left( {SCD} \right)\) và \(HK \not\subset \left( {SCD} \right)\).
Do đó \(HK\,{\rm{//}}\,\left( {SCD} \right)\).
+ Trong mặt phẳng \(\left( {SBD} \right)\) kẻ đường thẳng qua \(K\) và song song với \(SB\) cắt \(SD\) tại \(E\).
Trong mặt phẳng \(\left( {SCD} \right)\) kẻ đường thẳng qua \(E\) và song song với \(SC\) cắt \(CD\) tại \(F\).
Gọi \(G = KF \cap AB\); \(L = GH \cap SA\).
Khi đó ta có
\(\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {ABCD} \right) = GF\\\left( \alpha \right) \cap \left( {SAB} \right) = GL\\\left( \alpha \right) \cap \left( {SAD} \right) = LE\\\left( \alpha \right) \cap \left( {SCD} \right) = EF\end{array} \right.\)
\( \Rightarrow \) thiết diện của hình chóp \(S.ABCD\) khi cắt bởi mặt phẳng \(\left( \alpha \right)\) là hình thang \[EFGL\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.