Do xe máy bị hỏng, cô Bình quyết định đi làm bằng taxi. Trong ví của cô Bình lúc đó có \(450\,\,000\) đồng. Biết rằng, giá cước của taxi là \(11\,\,000\) đồng cho \(1{\rm{\;km}}\) đầu tiên và \(13\,\,000\) đồng cho những kilômét tiếp theo.

a) Gọi \(x\) (km, \(x > 0\)) là quãng đường mà cô Bình đi được. Từ dữ kiện đề bài hãy viết bất phương trình ẩn \(x\) phù hợp.

b) Tính quãng đường tối đa (làm tròn đến hàng đơn vị của kilômét) mà cô Bình có thể đi được.

Giá thuê mỗi phòng sau khi tăng giá phòng lên \[x\% \] là: \(480 + 480 \cdot x\%  = 480 + 4,8x\) (nghìn đồng).

Số phòng cho thuê lúc giá phòng tăng \[x\% \] là: O10-2024-GV154..\[100 - 100 \cdot \frac{{4x}}{5}\% \]\[ = 100 - \frac{{4x}}{5}\] (phòng).

Tổng doanh thu tương ứng là:

\[A\left( x \right) = \left( {100 - \frac{{4x}}{5}} \right)\left( {480 + 4,8x} \right)\]\[ = 3,84\left( {125 - x} \right)\left( {100 + x} \right)\] (nghìn đồng).

Để nhà nghỉ đạt doanh thu cao nhất thì ta tìm giá trị lớn nhất của biểu thức \(A\left( x \right)\).

⦁ Chứng minh bất đẳng thức: \(ab \le {\left( {\frac{{a + b}}{2}} \right)^2}\,\,\,\,\left( * \right)\) với \(a,\,\,b\) là các số không âm.

Thật vậy, xét hiệu \({\left( {\frac{{a + b}}{2}} \right)^2} - ab = \frac{{{a^2} + 2ab + {b^2} - 4ab}}{4} = \frac{{{a^2} - 2ab + {b^2}}}{4} = \frac{{{{\left( {a - b} \right)}^2}}}{2}\)

Với mọi \(a,\,\,b\) là các số không âm, ta có:

\({\left( {a - b} \right)^2} \ge 0\) nên \(\frac{{{{\left( {a - b} \right)}^2}}}{2} \ge 0\) suy ra \({\left( {\frac{{a + b}}{2}} \right)^2} \ge ab\).

Dấu “=” xảy ra khi và chỉ khi \(a = b.\) Như vậy bất đẳng thức \(\left( * \right)\) đã được chứng minh.

⦁ Áp dụng bất đẳng thức \(\left( * \right)\) cho biểu thức \(A\left( x \right) = 3,84\left( {125 - x} \right)\left( {100 + x} \right),\) ta được:

\[A\left( x \right) = 3,84\left( {125 - x} \right)\left( {100 + x} \right) \le 3,84 \cdot {\left( {\frac{{125 - x + 100 + x}}{2}} \right)^2} = 48\,\,600\].

Dấu “=” xảy ra khi và chỉ khi \[125 - x = 100 + x\] hay \[x = 12,5\].

Vậy giá phòng niêm yết là \[480 + 4,8 \cdot 12,5 = 540\] (nghìn đồng) thì khách sạn đạt doanh thu cao nhất là \(48\,\,600\) nghìn đồng \((48\,\,600\,\,000\) đồng).

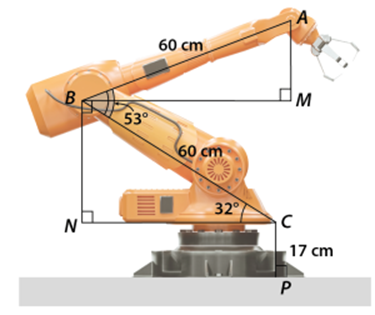
Xét \(\Delta BCN\) vuông tại \(N,\) ta có:

\(BN = BC \cdot \sin \widehat {BCN} = 60 \cdot \sin 32^\circ  \approx 31,80{\rm{\;(cm)}}{\rm{.}}\)

Ta thấy \(NC\) và \(BM\) là các đoạn thẳng nằm trên phương ngang nên \(NC\,{\rm{//}}\,BM,\) suy ra \(\widehat {CBM} = \widehat {BCN} = 32^\circ \) (so le trong).

Khi đó, \(\widehat {ABM} = \widehat {ABC} - \widehat {CBM} = 53^\circ  - 32^\circ  = 21^\circ \).

Xét \(\Delta ABM\) vuông tại \(M\), ta có:

\(AM = AB \cdot \sin \widehat {ABM} = 60 \cdot \sin 21^\circ  \approx 21,50\) (cm).

Vậy, độ cao của điểm \(A\) trên đầu cánh tay robot so với mặt đất là:

\(AM + BN + CP \approx 21,50 + 31,80 + 17 = 70,3\) (cm).