Cô Nhiên muốn xây dựng một bể nước hình chữ nhật để tòa nhà dùng chung. Biết bể nước hình chữ nhật có tổng chiều dài và chiều rộng của bể là 60 m. Tính diện tích lớn nhất lớn nhất của bể nước đó (giả sử chiều dày của thành bể không đáng kể).

Xem lời giải

Câu hỏi trong đề: Bộ 5 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi \(x,\,\,y\) lần lượt là chiều dài và chiều rộng của bể nước hình chữ nhật \(\left( {x > 0,\,\,y > 0} \right).\)

Tổng chiều dài và chiều rộng của bể là 60 m nên ta có \[x + y = 60\,\,\left( {\rm{m}} \right).\]

Diện tích bể nước là: \(xy\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right){\rm{.}}\)

⦁ Chứng minh bất đẳng thức: \[ab \le {\left( {\frac{{a + b}}{2}} \right)^2}\,\,\,\,\left( * \right)\] với \(a,\,\,b\) là các số không âm.

Thật vậy, xét hiệu \({\left( {\frac{{a + b}}{2}} \right)^2} - ab = \frac{{{a^2} + 2ab + {b^2} - 4ab}}{4} = \frac{{{a^2} - 2ab + {b^2}}}{4} = \frac{{{{\left( {a - b} \right)}^2}}}{2}\)

Với mọi \(a,\,\,b\) là các số không âm, ta có:

\({\left( {a - b} \right)^2} \ge 0\) nên \(\frac{{{{\left( {a - b} \right)}^2}}}{2} \ge 0\) suy ra \({\left( {\frac{{a + b}}{2}} \right)^2} \ge ab\).

Dấu “=” xảy ra khi và chỉ khi \(a = b.\) Như vậy bất đẳng thức \(\left( * \right)\) đã được chứng minh.

⦁ Áp dụng bất đẳng thức \(\left( * \right)\) ta được:

\[xy \le {\left( {\frac{{x + y}}{2}} \right)^2} = {\left( {\frac{{80}}{2}} \right)^2} = 1\,\,600.\]

Dấu “=” xảy ra khi và chỉ khi \(x = y\) và \[x + y = 60\] hay \[{x^2} = 1\,\,600\] tức là \(x = y = 40.\)

Vậy diện tích lớn nhất của mảnh vườn là \(1\,\,600{\rm{\;}}{{\rm{m}}^2}.\)

Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Người ta cần lắp đặt một thiết bị chiếu sáng gắn trên tường cho một phòng triển lãm như hình vẽ. Thiết bị này có góc chiếu sáng là \(20^\circ \) và cần đặt cao hơn mặt đất là \(2,5\,\,{\rm{m}}.\) Người ta đặt thiết bị chiếu sáng này sát tường và được căn chỉnh sao cho trên mặt đất dải ánh sáng bắt đầu từ vị trí cách tường \(2\,\,{\rm{m}}\) (như hình vẽ).

Xem đáp án

Lời giải

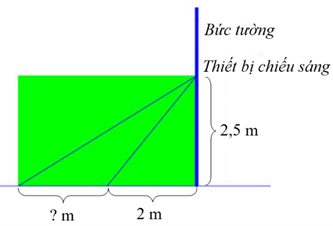
Xét \(\Delta ABC\) vuông tại \(B\), ta có

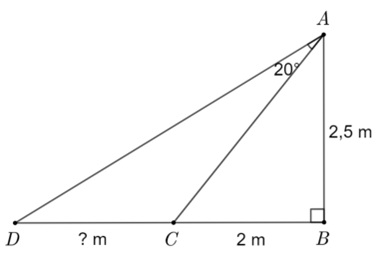
Người ta cần lắp đặt một thiết bị chiếu sáng gắn trên tường cho một phòng triển lãm như hình vẽ. (ảnh 2)

\(\tan \widehat {BAC} = \frac{{BC}}{{AB}} = \frac{2}{{2,5}} = 0,8\) nên \(\widehat {BAC} \approx 38,7^\circ .\)

Ta có \(\widehat {BAD} = \widehat {BAC} + \widehat {CAD} \approx 38,7^\circ + 20^\circ = 58,7^\circ .\)

Xét \(\Delta ABD\) vuông tại \(B\), ta có

\(BD = AB \cdot \tan \widehat {BAD} \approx 2,5 \cdot \tan 58,7^\circ \approx 4,1\,\,\left( {\rm{m}} \right).\)

Do đó \(CD = BD - BC \approx 4,1 - 2 = 2,1\,\,\left( {\rm{m}} \right).\)

Vậy độ dài vùng được chiếu sáng trên mặt đất khoảng \(2,1\) mét.

Câu 2

Người ta dùng một loại xe tải để chở sữa tươi cho một nhà máy. Biết mỗi thùng sữa loại \(180\,\,{\rm{ml}}\) nặng trung bình \(10\,\,{\rm{kg}}.\) Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là \(5,25\) tấn.

a) Gọi \(x\) là số thùng sữa mà xe có thể chở \(\left( {x \in \mathbb{N}*} \right)\). Viết bất phương trình phù hợp với dữ liệu đề bài.

b) Hỏi xe có thể chở được tối đa bao nhiêu thùng sữa như vậy, biết bác lái xe nặng \(65\,\,kg?\)

Xem đáp án

Lời giải

a) Đổi \(5,25\) tấn \( = 5\,\,250\,\,{\rm{kg}}\).

Gọi \(x\) (thùng) là số sữa mà xe có thể chở \(\left( {x \in \mathbb{N}*} \right)\).

Khi đó, khối lượng sữa mà xe chở là: \(10x\,\,\left( {{\rm{kg}}} \right).\)

Tổng khối lượng sữa và bác tài xế là: \(65 + 10x\,\,\left( {{\rm{kg}}} \right).\)

Do trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là \(5\,\,250\,\,{\rm{kg}}\) nên ta có

\(65 + 10x \le 5\,\,250\)

Vậy bất phương trình cần tìm là: \(65 + 10x \le 5\,\,250\).

b) Giải bất phương trình:

\(65 + 10x \le 5\,\,250\)

\(10x \le 5\,\,185\)

\(x \le 518,5\)

Mà \(x \in \mathbb{N}*\) nên xe tải đó có thể chở tối đa 518 thùng sữa.

Câu 3