Giả sử một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hoá bởi hàm số \(h\left( t \right) = 120\cos \left( {\frac{\pi }{{12}}t} \right)\), trong đó h(t) là độ cao tính bằng centimet trên mực nước biển trung bình tại thởi điểm t giây. Hỏi sau thời gian ít nhất bao nhiêu thì đỉnh của sóng sẽ lại chạm vào cột và tính chiều cao của sóng (khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng).
Quảng cáo
Trả lời:
Gọi T là chu kỳ của hàm \(h\left( t \right) = 120\cos \left( {\frac{\pi }{{12}}t} \right)\)
\(\begin{array}{l}h\left( {t + T} \right) = h(t) \Leftrightarrow 120\cos \left( {\frac{\pi }{{12}}t + \frac{\pi }{{12}}T} \right) = 120\cos \left( {\frac{\pi }{{12}}t} \right)\\ \Leftrightarrow \cos \left( {\frac{\pi }{{12}}t + \frac{\pi }{{12}}T} \right) = \cos \left( {\frac{\pi }{{12}}t} \right)(1)\end{array}\)
Mặt khác ta lại có \(\cos \left( {\frac{\pi }{{12}}t + k2\pi } \right) = \cos \left( {\frac{\pi }{{12}}t} \right)(2)\)
Từ (1) và (2) suy ra \(\frac{\pi }{{12}}T = k2\pi \Leftrightarrow T = k24\)
Do T là số dương nhỏ nhất nên k = 1
Vậy chu kỳ của sóng là T = 24
Do đó sau khoảng thời gian 24s thì con sóng được lặp lại, hay đỉnh của sóng lại chạm vào cột.
- Chiều cao của sóng là \(h = \left| {Maxh(t)} \right| + \left| {Minh\left( t \right)} \right| = 240cm\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn C
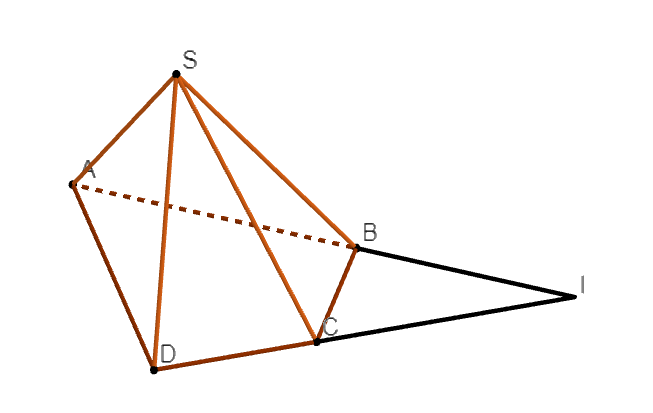
M, N lần lượt là trung điểm của SA và SB nên MN là đường trung bình của tam giác SAB
\( \Rightarrow MN//AB\) mà \(AB//CD \Rightarrow MN//CD \Rightarrow MN//(SCD)\).
Lời giải
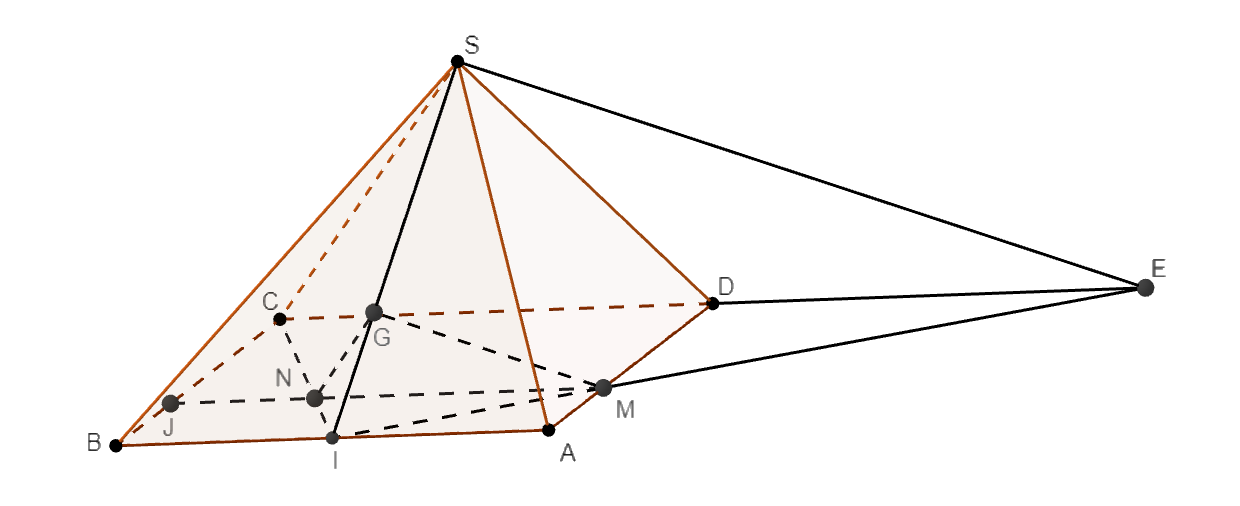
a. Gọi J là giao điểm của MN với BC
Ta có \[\frac{{IN}}{{IC}} = \frac{{BJ}}{{BC}} = \frac{{AM}}{{AD}} = \frac{1}{3}\],\[\frac{{IG}}{{IS}} = \frac{1}{3}\]
\[ \Rightarrow \frac{{IN}}{{IC}} = \frac{{IG}}{{IS}} \Rightarrow NG\parallel SC\]
mà \[SC \subset \left( {SCD} \right)\]
\[ \Rightarrow NG\parallel \left( {SCD} \right)\].
b. Gọi \[E\] là giao điểm của \[IM\] và \[CD\]
Ta có \[\frac{{IM}}{{IE}} = \frac{{AM}}{{AD}} = \frac{1}{3} \Rightarrow \frac{{IM}}{{IE}} = \frac{{IG}}{{IS}}\]
\[ \Rightarrow MG\parallel SE\], \[SE \subset \left( {SCD} \right) \Rightarrow GM\parallel \left( {SCD} \right)\].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.