Trong các mệnh đều sau, mệnh đề nào sai?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn D
Ta có: \(\cos x = \cos \frac{\pi }{4} \Leftrightarrow x = \pm \frac{\pi }{4} + k2\pi ,{\rm{ }}(k \in \mathbb{Z})\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
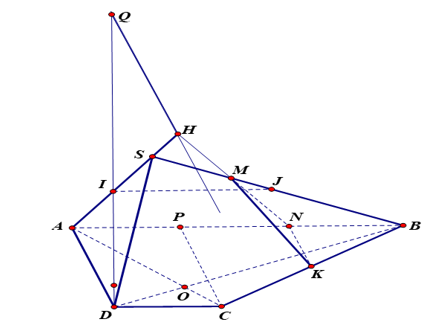
a) Tìm giao tuyến của \(\left( {SAC} \right)\) và \(\left( {SBD} \right).\)
\[S \in (SAC) \cap (SBD)\,\,(1)\]
\[\begin{array}{l}Trong\,(ABCD)\,:AC \cap \,BD = O\\\left\{ \begin{array}{l}O \in AC \Rightarrow O \in (SAC)\\O \in BD \Rightarrow O \in (SBD)\end{array} \right. \Rightarrow O \in (SAC) \cap (SBD)\,\,(2)\end{array}\]
Từ \[\,(1),\,(2)\,\] \[ \Rightarrow (SAC) \cap (SBD) = SO\].
b) Chứng minh \[IJ\parallel \left( {SCD} \right)\].
Ta có\[\,IJ \not\subset (SCD)\,(3)\]
\(CD \subset (SCD)\,(4)\)
Mà\[{\rm{ }}IJ\parallel AB\,\,\](\[IJ\,\]là đường trung bình của \[\Delta SAB\]),\[CD\parallel AB\,\,\]( giả thiết ) \[ \Rightarrow IJ\parallel CD\,(5)\]
Từ \[\,(3),\,(4)\,,(5)\] \[ \Rightarrow IJ{\rm{//}}(SCD)\].
c) Xác định giao điểm của \(ID\) và mặt phẳng \(\left( {MNK} \right)\).
*\[Trong\,\left( {SAB} \right)\,:SA \cap \,MN = H \Rightarrow H \in \left( {SAD} \right) \cap \left( {MNK} \right)\,\,(6)\]
Lấy \[P\,\]là trung điểm\[AN\].
\[{\rm{ + }}KN\parallel CP\,\,\](\[KN\]là đường trung bình của \[\Delta BCP\] ) ,\[CP\parallel AD\,\,\]( \[APCD\] là hình bình hành vì có cặp cạnh đối \[AP\] và \[CD\]song song và bằng nhau ) \[ \Rightarrow KN\parallel AD\,(7)\]
+\[\left\{ \begin{array}{l}{\rm{KN}} \subset \left( {KMN} \right)\\AD \subset \left( {SAD} \right)\end{array} \right.(8)\]
Từ \[(\,6),(7),(8)\] \[ \Rightarrow \left( {SAD} \right) \cap \left( {MNK} \right) = d(d\,\,qua\,H,d{\rm{//}}AD,{\rm{//}}KN)\]
\[\begin{array}{l} + DI \subset \left( {SAD} \right)\\ + \left( {SAD} \right) \cap \left( {MNK} \right)\, = d\\ + DI \cap d = Q\\\left\{ \begin{array}{l}Q \in DI\\Q \in d \subset \left( {MNK} \right) \Rightarrow Q \in \left( {MNK} \right)\end{array} \right. \Rightarrow DI \cap \left( {MNK} \right) = Q\end{array}\]
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập