(1,5 điểm) Cho hình chóp \(S.ABCD\) có đáy là hình bình hành \(ABCD\). Gọi \(M,N,P\) lần lượt là trung điểm của cạnh \(SA,\,AD,\,BC\).
a) Xác định giao tuyến của mặt phẳng \(\left( {SAB} \right)\) và \(\left( {CMN} \right)\).
b) Chứng minh đường thẳng \(MN\) song song với mặt phẳng \(\left( {SCD} \right)\).
c) Xác định \(K\) là giao điểm của đường thẳng \(MP\) và mặt phẳng \(\left( {SBN} \right)\). Tính tỷ số \(\frac{{MK}}{{KP}}\).
(1,5 điểm) Cho hình chóp \(S.ABCD\) có đáy là hình bình hành \(ABCD\). Gọi \(M,N,P\) lần lượt là trung điểm của cạnh \(SA,\,AD,\,BC\).
a) Xác định giao tuyến của mặt phẳng \(\left( {SAB} \right)\) và \(\left( {CMN} \right)\).
b) Chứng minh đường thẳng \(MN\) song song với mặt phẳng \(\left( {SCD} \right)\).
c) Xác định \(K\) là giao điểm của đường thẳng \(MP\) và mặt phẳng \(\left( {SBN} \right)\). Tính tỷ số \(\frac{{MK}}{{KP}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
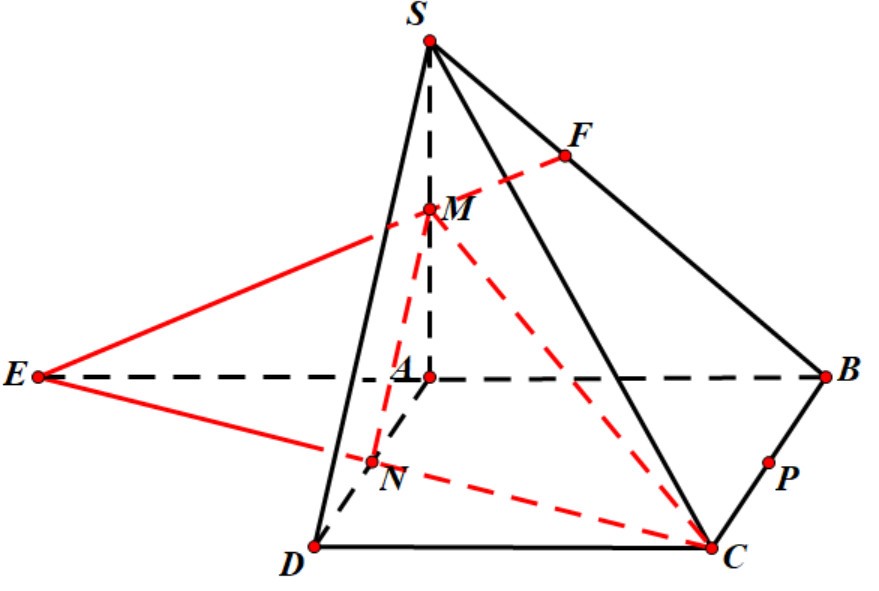
a) Ta có
\(\left. \begin{array}{l}M \in \left( {CMN} \right)\\M \in SA \subset \left( {SAB} \right)\end{array} \right\} \Rightarrow \left( {CMN} \right) \cap \left( {SAB} \right)\,\,\left( 1 \right)\)
Trong mp\(\left( {ABCD} \right)\) kéo dài \(CN \cap AB \equiv E\)
\( \Rightarrow \left. \begin{array}{l}E \in CN \subset \left( {CMN} \right)\\E \in AB \subset \left( {SAB} \right)\end{array} \right\} \Rightarrow E \in \left( {CMN} \right) \cap \left( {SAB} \right)\,\,\left( 2 \right)\)
Từ (1) và (2) ta có \(\left( {CMN} \right) \cap \left( {SAB} \right)\, = ME\)
Hay \(\left( {CMN} \right) \cap \left( {SAB} \right)\, = MF\,\,\left( {F = EM \cap SB} \right)\)
b) Ta có:
\(\left. \begin{array}{l}MN \not\subset \left( {SCD} \right)\\MN{\rm{//}}SD\\SD \subset \left( {SCD} \right)\end{array} \right\} \Rightarrow MN{\rm{//}}\left( {SCD} \right)\)
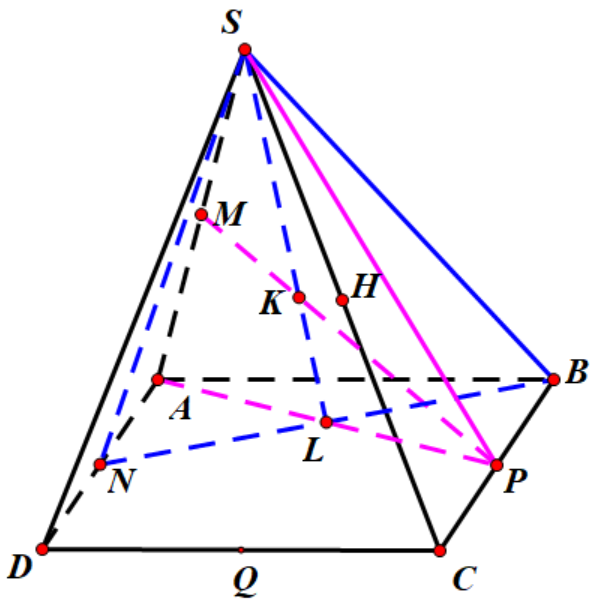
c) Ta có trong \(\left( {ABCD} \right):AP \cap BN \equiv L\)\( \Rightarrow L\) là trung điểm của \(AP\)
Trong \(\left( {SAP} \right):SL \cap MP \equiv K\)
\( \Rightarrow K\)là trọng tâm tam giác \(SAP\)
\( \Rightarrow \frac{{MK}}{{KP}} = \frac{1}{2}\)
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn B
Ta có \(\tan x = - 1 \Leftrightarrow \tan x = \tan \left( { - \frac{\pi }{4}} \right) \Leftrightarrow x = - \frac{\pi }{4} + k\pi ,\,\,k \in \mathbb{Z}\).
Câu 2
Lời giải
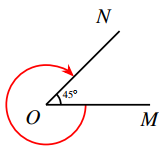
Chọn A
Dựa vào hình biểu diễn ta có \({\rm{s\~n }}\left( {OM\,,\,ON} \right) = - 135^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Chọn C Ta có \[\frac{\pi }{2} < a < \pi \] thì \[\sin a > 0\], \[cosa < 0\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/3-1764212832.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập