Cho lăng trụ \(ABC.A'B'C'\). Gọi \(M\) là trung điểm của \(AC\). Khi đó hình chiếu song song của điểm \(M\) lên \(\left( {AA'B'} \right)\) theo phương chiếu \(CB\) là
Quảng cáo
Trả lời:
Chọn C
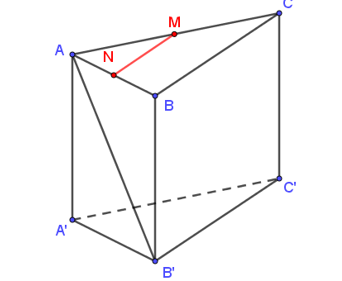
Ta có: \[\left( {AA'B'} \right) \equiv \left( {ABB'A'} \right)\].
Gọi \[N\] là trung điểm của \[AB\]\[ \Rightarrow MN\parallel AB\].
Vậy \[N\] là hình chiếu chiếu song song của điểm \(M\) lên \(\left( {AA'B'} \right)\) theo phương chiếu \(CB\) .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn A
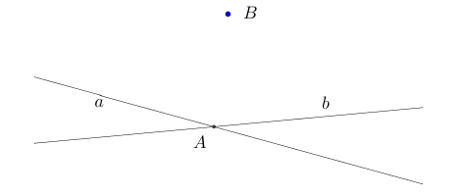
Ta xác định được \(3\) mặt phẳng là: \(\left( {a,b} \right)\); \(\left( {B,a} \right)\); \(\left( {B,b} \right)\).
Lời giải
a) Ta có:
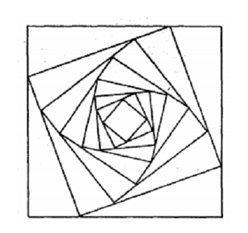
\({s_1} = {a^2}\), Cạnh của hình vuông là: .
Do đó diện tích .
Cạnh của hình vuông (C3) là: 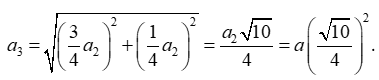
Do đó diện tích 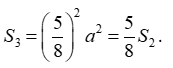
Tương tự ta có :\({s_1},{s_2},...,{s_n},...\)Lập thành csn lùi vô hạn có số hạng đầu là :\({s_1} = {a^2}\), công bội \(q = \frac{5}{8}\)
Vậy: \(T = {s_1} + {s_2} + {s_3} + ... + {s_n} + ... = \frac{{{s_1}}}{{1 - q}} = \frac{{{a^2}}}{{1 - \frac{5}{8}}} = \frac{{8{a^2}}}{3} = \frac{{32}}{3} \Leftrightarrow a = 2\)
b) Sau \(1\) tháng giá trị của ô tô còn lại là:
\[{u_1}\; = {\rm{ 7}}00{\rm{ }}--{\rm{ 7}}00.0,4\% {\rm{ }} = {\rm{ 7}}00.\left( {1{\rm{ }}--{\rm{ 0,}}4\% } \right){\rm{ }}\](triệu đồng).
Sau \(2\) tháng giá trị của ô tô còn lại là:
\[{u_2}\; = {\rm{ 7}}00.\left( {1{\rm{ }}--{\rm{ 0,}}4\% } \right){\rm{ }}--{\rm{ 7}}00.\left( {1{\rm{ }}--{\rm{ 0,}}4\% } \right).0,4\% {\rm{ }} = {\rm{ 7}}00.{\left( {1{\rm{ }}--{\rm{ 0,}}4\% } \right)^2}\;\] (triệu đồng).
Sau \(3\) tháng giá trị của ô tô còn lại là:
\[{u_3}\; = {\rm{ 7}}00.{\left( {1{\rm{ }}--{\rm{ 0,}}4\% } \right)^2}{\rm{ }}--{\rm{ 7}}00.{\left( {1{\rm{ }}--{\rm{ 0,}}4\% } \right)^2}.0,4\% {\rm{ }} = {\rm{ 7}}00.{\left( {1{\rm{ }}--{\rm{ 0,}}4\% } \right)^3}\;\](triệu đồng).
Gọi \({u_n}\) là giá trị của ô tô sau \(n\) tháng sử dụng.
Dãy số \(\left( {{u_n}} \right)\) tạo thành một cấp số nhân với số hạng đầu là giá trị đầu của ô tô là\[{u_1}\; = {\rm{7}}00.\left( {1{\rm{ }}--{\rm{ 0,}}4\% } \right){\rm{ }}\]triệu đồng và công bội \[q = 1{\rm{ }}--{\rm{ 0,}}4\% {\rm{ }}\].
Khi đó công thức tổng quát để tính \[{u_n}\; = {\rm{7}}00.{\left( {1{\rm{ }}--{\rm{ 0,}}4\% } \right)^n}{\rm{ }}\].
Sau \(3\) năm sử dụng giá trị của ô tô còn lại là:\[{u_{36}}\; = {\rm{ 7}}00.{\left( {1{\rm{ }}--{\rm{ 0,}}4\% } \right)^{36}}\; \approx {\rm{ 605,95}}\] (triệu đồng).
Sau \(3\) năm thầy Thu làm ra \(18.36 = 648\) (triệu đồng).
Sau \(3\) năm tổng số tiền (bao gồm giá tiền xe ô tô và tổng số tiền thầy Thu làm ra) thầy Thu có được là \(648 + 605,95 = 1253,95\)(triệu đồng).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.