Cho các số thực a, b, c thỏa mãn \[4a + c > 8 + 2b\] và \[a + b + c < - 1\]. Khi đó số nghiệm thực phân biệt của phương trình \[{x^3} + a{x^2} + bx + c = 0\] bằng
Cho các số thực a, b, c thỏa mãn \[4a + c > 8 + 2b\] và \[a + b + c < - 1\]. Khi đó số nghiệm thực phân biệt của phương trình \[{x^3} + a{x^2} + bx + c = 0\] bằng
Quảng cáo
Trả lời:
Chọn C
Xét phương trình: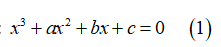
Đặt: \[f\left( x \right) = {x^3} + a{x^2} + bx + c\]
Từ giả thiết \[\left\{ \begin{array}{l}4a + c > 8 + 2b \Rightarrow - 8 + 4a - 2b + c > 0\\a + b + c < - 1 \Rightarrow 1a + b + c < 0 \Rightarrow f\left( 1 \right) < 0\end{array} \right.\]
Do đó \[f\left( { - 2} \right).f\left( 1 \right) < 0\] nên phương trình (1) có ít nhất một nghiệm trong \[\left( { - 2;\,\,1} \right)\]
Ta nhận thấy:
\[\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty \] mà \[f\left( { - 2} \right) > 0\] nên phương trình (1) có ít nhất một nghiệm \[\alpha \in \left( { - \infty ;\,\, - 2} \right)\]
Tương tự: \[\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \] mà \[f\left( 1 \right) < 0\] nên phương trình (1) có ít nhất một nghiệm \[\beta \in \left( {1;\,\, + \infty } \right)\]
Như vậy phương trình đã cho có ít nhất 3 nghiệm thực phân biệt, mặt khác phương trình bậc 3 có tối đa 3 nghiệm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn C
Dựa vào bảng số liệu đã cho thì có \[47\] nhân viên trong công ty nhận được mức thưởng tết từ 15 triệu đồng đến dưới 20 triệu đồng.
Câu 2
Lời giải
Chọn D
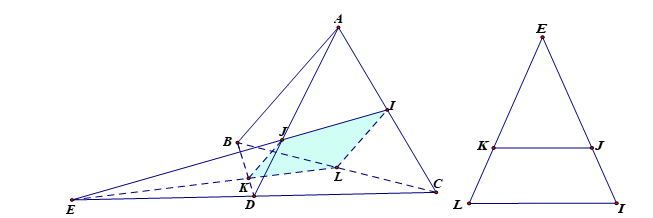
Gọi \(K = \left( P \right) \cap BD\), \(L = \left( P \right) \cap BC\), \(E = \left( P \right) \cap CD\).
Vì \(\left( P \right)\,\,//\,AB\) nên \(IL\,//\,AB\), \(JK\,//\,AB\). Do đó \(IJKL\) hình thang và \(L\) là trung điểm cạnh \(BC\), nên ta có \(\frac{{KD}}{{KB}} = \frac{{JD}}{{JA}} = \frac{1}{2}\).
Xét tam giác \(ACD\) có \(I\), \(J\), \(E\) thẳng hàng. Áp dụng định lí Mê-nê-la-uýt ta có:
\(\frac{{ED}}{{EC}}.\frac{{IC}}{{IA}}.\frac{{JA}}{{JD}} = 1 \Rightarrow \frac{{ED}}{{EC}} = \frac{1}{2} \Rightarrow D\) là trung điểm \(EC\).
Dễ thấy hai tam giác \(ECI\) và \(ECL\) bằng nhau theo trường hợp c-g-c.
Áp dụng định lí cosin cho tam giác \(ICE\) ta có:
\(E{I^2} = E{C^2} + I{C^2} - 2EC.IC.\cos 60^\circ = \frac{{13{a^2}}}{4}\)\( \Rightarrow EL = EI = \frac{{a\sqrt {13} }}{2}\).
Áp dụng công thức Hê-rông cho tam giác \(ELI\) ta có: \({S_{ELI}} = \sqrt {p{{\left( {p - x} \right)}^2}\left( {p - y} \right)} = \frac{{\sqrt {51} }}{{16}}{a^2}\)
Với \(p = \frac{{EI + EL + IL}}{2} = \frac{{2\sqrt {13} + 1}}{4}a\), \(x = EI = EL = \frac{{\sqrt {13} }}{2}a\), \(y = IL = \frac{a}{2}\).
Hai tam giác \(ELI\) và tam giác \(EKJ\) đồng dạng với nhau theo tỉ số \(k = \frac{2}{3}\) nên
Do đó: \({S_{IJKL}} = {S_{ELI}} - {S_{EKJ}} = {S_{ELI}} - {\left( {\frac{2}{3}} \right)^2}{S_{ELI}} = \frac{{5\sqrt {51} }}{{144}}{a^2}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
