Cho hình chữ nhật ABCD. Trên cạnh AB lấy điểm M và N sao cho AM = MN = NB.
a) Tính: \(\frac{{{S_{AMCD}}}}{{{S_{NBCD}}}}\)
b) Tính: \(\frac{{{S_{AMCD}}}}{{{S_{ABCD}}}}\)
Cho hình chữ nhật ABCD. Trên cạnh AB lấy điểm M và N sao cho AM = MN = NB.
a) Tính: \(\frac{{{S_{AMCD}}}}{{{S_{NBCD}}}}\)
b) Tính: \(\frac{{{S_{AMCD}}}}{{{S_{ABCD}}}}\)Câu hỏi trong đề: 2 bài tập Bài toán về hình thang có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng Dẫn Giải
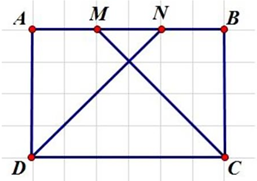
a) Ta có: \({S_{AMCD}} = \frac{{(AM + CD) \times AD}}{2}\) và \({S_{NBCD}} = \frac{{(BN + CD) \times BC}}{2}\)
Mà AM = BN và AD = BC nên \({S_{AMCD}} = {S_{NBCD}} \to \frac{{{S_{AMCD}}}}{{{S_{NBCD}}}} = 1\).
b) Theo đề bài ta có: \(AM = \frac{1}{3} \times AB\)
\( \to {S_{AMCD}} = \frac{{(AM + CD) \times AD}}{2} = \frac{{\left( {\frac{1}{3} \times AB + AB} \right) \times AD}}{2} = \frac{2}{3} \times AB \times AD = \frac{2}{3} \times {S_{ABCD}}\)
Vậy \(\frac{{{S_{AMCD}}}}{{{S_{ABCD}}}} = \frac{2}{3}\)
Đáp Số: a) 1 b) \(\frac{2}{3}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng Dẫn Giải
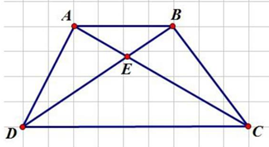
Ta có:
\({S_{ACD}} = {S_{BCD}}\) (chung đáy CD và chiều cao tương ứng bằng chiều cao hình thang ABCD)
\({S_{DAB}} = {S_{CAB}}\) (chung đáy AB và chiều cao tương ứng bằng chiều cao hình thang ABCD)
Lại có: \({S_{ACD}} = {S_{EAD}} + {S_{ECD}}\) và \({S_{BCD}} = {S_{EBC}} + {S_{ECD}}\). Suy ra: \({S_{EAD}} = {S_{EBC}}\).
Vậy các cặp tam giác bằng nhau là: \({S_{ACD}} = {S_{BCD}}\); \({S_{DAB}} = {S_{CAB}}\); \({S_{EAD}} = {S_{EBC}}\)
Đáp Số: \({S_{ACD}} = {S_{BCD}}\); \({S_{DAB}} = {S_{CAB}}\); \({S_{EAD}} = {S_{EBC}}\)
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập