Cho hình thang ABCD (hình vẽ). Biết diện tích các tam giác AED là \(2{\rm{c}}{{\rm{m}}^2}\) và BFC là \(3{\rm{c}}{{\rm{m}}^2}\). Tính diện tích tứ giác MENF
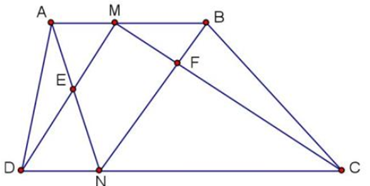
Cho hình thang ABCD (hình vẽ). Biết diện tích các tam giác AED là \(2{\rm{c}}{{\rm{m}}^2}\) và BFC là \(3{\rm{c}}{{\rm{m}}^2}\). Tính diện tích tứ giác MENF
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng Dẫn Giải
Ta có: \({S_{ADN}} = {S_{MDN}}\) (cùng đáy DN và có chiều cao bằng nhau)
\( \Rightarrow {S_{AED}} + {S_{EDN}} = {S_{MEN}} + {S_{EDN}} \Rightarrow {S_{ADE}} = {S_{MEN}} \Rightarrow {S_{MEN}} = 2{\rm{ c}}{{\rm{m}}^2}\)
Tương tự cũng có: \({S_{MCN}} = {S_{BCN}}\)
\( \Rightarrow {S_{MFN}} + {S_{FCN}} = {S_{BFC}} + {S_{FCN}} \Rightarrow {S_{MFN}} = {S_{BFC}} \Rightarrow {S_{MFN}} = 3{\rm{ c}}{{\rm{m}}^2}\)
Mà: \({S_{MENF}} = {S_{MEN}} + {S_{MFN}} \Rightarrow {S_{MEFN}} = 2 + 3 = 5{\rm{ c}}{{\rm{m}}^2}\)
Đáp Số: \(5{\rm{ c}}{{\rm{m}}^2}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
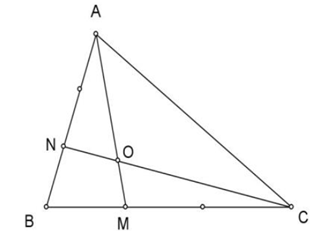
Hướng Dẫn Giải
\({S_{OBN}} = \frac{1}{2}{S_{OAN}} = 4{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
\({S_{OAC}} = 2{S_{OAB}} = 2 \times 12 = 24{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Ta có: \({S_{OMC}} = 2{S_{OBM}}\) và \({S_{OAC}} = 2{S_{OBC}}\)
\( \Rightarrow {S_{OAC}} = 2 \times ({S_{OMC}} + {S_{OBM}}) = 2 \times (2 \times {S_{OBM}} + {S_{OBM}}) = 6 \times {S_{OBM}}\)
\( \Rightarrow {S_{OBM}} = 24:6 = 4{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Vậy \({S_{BNOM}} = 4 + 4 = 8{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Đáp Số: \(8{\rm{ c}}{{\rm{m}}^2}\)
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập