(3,0 điểm)

1) Cho hình chóp tứ giác đều có diện tích xung quanh là \(858,4{\rm{\;c}}{{\rm{m}}^2},\) đường cao của mặt bên xuất phát từ đỉnh dài \(18,66{\rm{\;cm}}.\) Tính độ dài cạnh đáy và cạnh bên của hình chóp (làm tròn kết quả đến chữ số thập phân thứ hai).

2) Cho hình bình hành \[ABCD\] có \[BC = 2AB.\] Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của \[BC,{\rm{ }}AD.\]

a) Chứng minh tứ giác \[MBND\] là hình bình hành.

b) Gọi \[P\] là giao điểm của \[AM\] và \[BN,{\rm{ }}Q\] là giao điểm của \[CN\] và \[DM.\] Chứng minh tứ giác \[PMQN\] là hình chữ nhật.

c) Tính diện tích của tứ giác \[PMQN,\] biết \[AB = 2{\rm{\;cm}},\] \(\widehat {MAD} = 30^\circ .\)

Hướng dẫn giải

1)

Theo bài, ta có trung đoạn \(d = 18,66{\rm{\;cm}}\) và diện tích xung quanh của hình chóp tứ giác đều là \({S_{xq}} = 858,4{\rm{\;c}}{{\rm{m}}^2}.\)

Do đó độ dài cạnh đáy của hình chóp là:

\(CD = \frac{{{S_{xq}}}}{{2d}} = \frac{{858,4}}{{2 \cdot 18,66}} \approx 23{\rm{\;}}\left( {{\rm{cm}}} \right).\)

Tam giác \(SCD\) cân tại \(S\) nên \(SI\) vừa là đường cao, vừa là đường trung tuyến.

Do đó \(CI = DI = \frac{{CD}}{2} \approx \frac{{23}}{2} = 11,5{\rm{\;}}\left( {{\rm{cm}}} \right).\)

Áp dụng định lí Pythagore cho tam giác vuông \(SCI,\) ta có:

\(S{C^2} = S{I^2} + I{C^2} \approx 18,{66^2} + 11,{5^2} = 480,4456\)

Suy ra \(SC \approx 21,92{\rm{\;}}\left( {{\rm{cm}}} \right).\)

Vậy độ dài cạnh bên của hình chóp tứ giác đều khoảng \(21,92{\rm{\;cm}}{\rm{.}}\)

2)

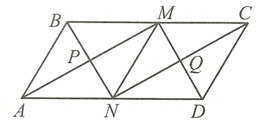
a) Do \[ABCD\] là hình bình hành nên \[BC\,{\rm{//}}\,AD\] và \[BC = AD.\]

Mà \[M \in BC,{\rm{ }}N \in AD\] nên \[MB\,{\rm{//}}\,ND\]

Lại có \[M,{\rm{ }}N\] lần lượt là trung điểm của \[BC,{\rm{ }}AD\] nên

\(MB = MC = \frac{1}{2}BC;NA = ND = \frac{1}{2}AD\)

Do đó \[MB = MC = NA = ND.\]

Tứ giác \[MBND\] có \[MB\,{\rm{//}}\,ND\] và \[MB = ND\] nên là hình bình hành.

b) Tương tự câu a, ta chứng minh được \[MANC\] là hình bình hành.

Do \[MBND,{\rm{ }}MANC\] đều là hình bình hành nên \[PN\,{\rm{//}}\,MQ,{\rm{ }}PM\,{\rm{//}}\,NQ\] (do \[P\] là giao điểm của \[AM\] và \[BN,{\rm{ }}Q\] là giao điểm của \[CN\] và \[DM).\]

Suy ra tứ giác \[PMQN\] là hình bình hành.

Xét \(\Delta ABN\) và \(\Delta MNB\) có:

\[AN = BM,\] \[\widehat {ANB} = \widehat {MBN}\](hai góc so le trong do \[BM\,{\rm{//}}\,AN),\] cạnh \[BN\] chung.

Do đó \(\Delta ABN = \Delta MNB\) (c.g.c). Suy ra \[AB = MN\] (hai cạnh tương ứng)

Tứ giác \[ABMN\] có \[AB = BM = MN = AN\] nên \[ABMN\] là hình thoi.

Suy ra \[AM \bot BN,\] do đó \(\widehat {MPN} = 90^\circ \).

Hình bình hành \[PMQN\] có \(\widehat {MPN} = 90^\circ \) nên \[PMQN\] là hình chữ nhật.

c) Ta có \[BM = AB = 2{\rm{\;cm}}.\]

Do \[ABMN\] là hình thoi nên \[AM\] là tia phân giác của \(\widehat {BAN}\).

Suy ra \(\widehat {BAN} = 2\widehat {MAD} = 60^\circ \).

Tam giác \[ABN\] có \[AB = AN\] và \(\widehat {BAN} = 60^\circ \) nên tam giác \[ABN\] đều.

Suy ra \[BN = AN = AB = 2{\rm{\;cm}}.\]

Do \[P\] là trung điểm của \[BN\] nên \(BP = NP = \frac{{BN}}{2} = 1{\rm{\;cm}}\).

Áp dụng định lý Pythagore cho tam giác \[BMP\] vuông tại \[P,\] ta có: \[B{M^2} = B{P^2} + M{P^2}.\]

Suy ra \[M{P^2} = B{M^2} - B{P^2} = {2^2} - {1^2} = 3.\] Do đó \(MP = \sqrt 3 {\rm{\;cm}}\).

Do \[PMQN\] là hình chữ nhật nên diện tích của \[PMQN\] là: \(MP.NP = \sqrt 3 .1 = \sqrt 3 \;\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)